1. Множество может быть задано перечислением всех его элементов. Например, если множество А состоит из элементов а, в, с, d, то оно записывается в виде: А= {а, в, с, d}. При этом порядок записи элементов в фигурных скобках не существен и каждый элемент записывается только один раз. Такой способ удобен при рассмотрении конечных множеств, содержащих небольшое число элементов, но иногда он может применяться и для задания бесконечных множеств, например {2, 4, 6, 8,…}. Естественно, что такая запись применима, если вполне ясно, что понимается под многоточием.
2. Описательный способ состоит в том, что указывается характерное свойство, которым обладают все элементы множества. Пусть М - область значений переменной x. Тогда множество А,состоящее из всех элементов x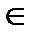 
М, обладающих свойством 
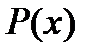задается в виде 
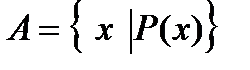, где x обозначается общий элемент множества, а P (x) - свойство, присущее всем элементам множества и только им. Например, пусть R - множество действительных чисел, тогда множество А действительных корней уравнения 
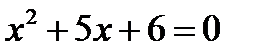может быть задано в виде: 
.
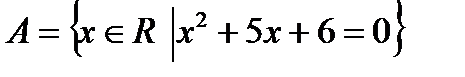В тех случаях, когда не вызывает сомнений, из какого множества берутся элементы х, указание о принадлежности х множеству М можно не делать. Например, множество простых чисел может быть задано в виде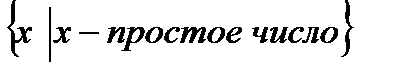 
. Вместо прямой черты часто используют двоеточие, например 
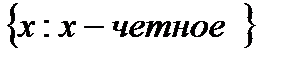- множество четных чисел. Описанием могут быть заданы как конечные, так и бесконечные множества.
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø. Например,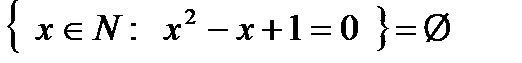 
.
Примеры пустых множеств: множество тупых углов равностороннего треугольника, множество действительных корней уравнения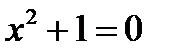 
, множество людей старше 300 лет.
Множество А является подмножеством множества В (А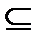 
В), если любой элемент множества А принадлежит множеству В
.
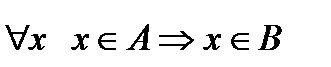Примеры подмножеств: множество натуральных чисел есть подмножество множества целых чисел; целые числа составляют подмножество множества действительных чисел; действительные числа составляют подмножество множества комплексных чисел.
Говорят также, что множество В включает в себя множество А. Знак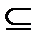 
нестрогого включения означает, что возможно равенство множеств: А=В. Если желают подчеркнуть, что В содержит и другие элементы, кроме элементов из множества А, то используют символ строгого включения 
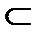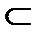: А В. Связь между символам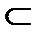и и 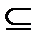дается выражением
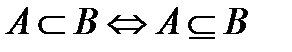и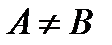 
.
В этом случае множество А называется истинным подмножеством В.
Множества А и В называются равными (А=В), если они состоят из одних и тех же элементов. В противном случае они называются неравными (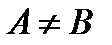
). Например, 
, 
.
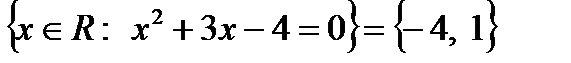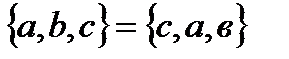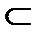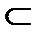Очевидно, равенство множеств равносильно одновременному выполнению условий А В и В А.
Пример. Пусть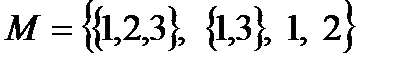 
. Верно ли, что
1. 
?
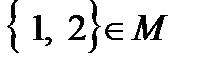2. 
?
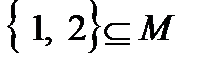Решение.
1. В первом случае множество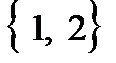 
рассматривается как элемент множества М. Но в множестве М нет такого элемента, следовательно 
.
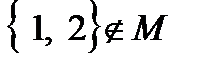2. Во втором случае множество 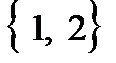рассматривается как подмножество множества М. Поскольку 
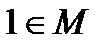и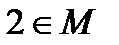 
, то по определению подмножества
.
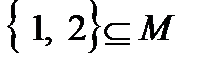В большинстве случаев можно считать, что все рассматриваемые множества являются подмножествами некоторого более обширного множества, которое называется универсальным и обозначается U(
). Следует отметить, что в различных конкретных рассмотрениях роль универсального множества могут играть различные множества. Так, при рассмотрении множеств студентов в группе (отличники; студенты, проживающие в общежитии; студенты, получающие стипендию, и т. п.) роль универсального множества играет множество студентов в группе.
Для изображения множеств используются диаграммы Эйлера-Венна. При этом универсальное множество изображается в виде прямоугольника, а его подмножества – в виде областей внутри этого прямоугольника (чаще всего окружностью или овалом).
Операции над множествами.
Операции над множествами называются теоретико-множественными операциями. Далее мы будем рассматривать все множества как подмножества некоторого универсального множества U.
1. Объединением множеств А и В называется множество С=А 
В, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, то есть С содержит все элементы множества А, все элементы множества В, в том числе и принадлежащие им обоим:
.
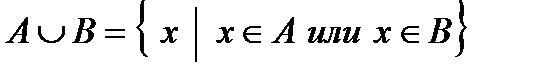На диаграмме Эйлера-Венна объединению соответствует заштрихованная область.
| А |
| В |
| В |
| А |
| А |
| В |
Пример 1. Если А ={1, 2, 3, 4, 5} и В ={2, 4, 6, 7}, то А В= {1, 2, 3, 4, 5, 6, 7}.
Пример 2. Если А - множество отличников в группе, а В - множество студентов, проживающих в общежитии, то А В- множество студентов, которые или учатся на отлично или проживают в общежитии.
2. Пересечением множеств А и В называется множество С=А 
В, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В, то есть С содержит элементы, являющиеся общими для множеств А и В:
.
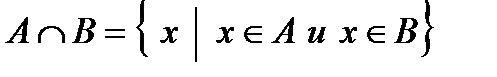| В |
| А |
| А |
| В |
| А |
| В |
Пример 3. Для множеств А и В в примере 1 А В ={2, 4}.
Пример 4. Для множеств А и В в примере 2 А В - множество отличников группы, проживающих в общежитии.
Наличие пустого множества Ø позволяет распространить операцию пересечения на множества, которые не имеют общих элементов. Если А 
В = Ø, то такие множества А и В называются непересекающимися.
Говорят, что множества А и В находятся в общем положении, если выполняются три условия:
1) существует элемент множества А,не принадлежащий В;
2) существует элемент множества В,не принадлежащий А;
3) существует элемент, принадлежащий как А, так и В.
3. Разностью множеств А и В называется множество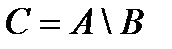 
, состоящее из всех тех и только тех элементов множества А, которые не принадлежат множеству В, т. е.
| А |
| В |
| А |
| В |
| А |
| В |
| А |
| В |
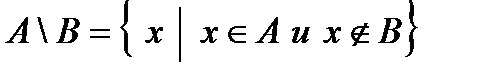, то есть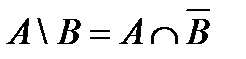 
Пример 5. Для множеств А и В в примере 1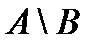 
={1, 3, 5}, 
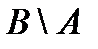={6, 7}. Если А и В множества из примера 2, то 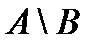- множество отличников, не проживающих в общежитии.
4. Дополнением множества А (до универсального множества U) называется множество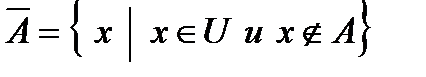 
.
| А |
| А |
Пример 6. Пусть U= { a,b,c,d,e }, А= { b,d }, тогда
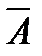={ a,c,e }.
5. Симметрической разностью множеств А и В называется множество С=А ∆ В, состоящее из всех тех и только тех элементов, которые принадлежат только множеству А или только множеству В, т. е.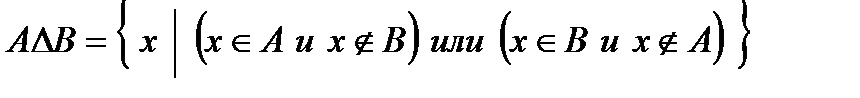 
| А |
| В |
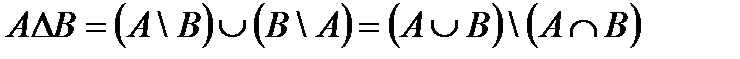
Пример 7. Пусть А ={ a,b,c }, В ={ c,d,e }, тогда А∆В ={ a,b,d,e }.
При А 
В= Ø симметрическая разность совпадает с их объединением.
