Методика вивчення табличного множення і ділення.
В 2-му класі учні разом з вчителем складали таблиці множення, а в 3-му класі їм надається виявити самостійність у складанні таблиць. Під час повторення матеріалу за 2-й клас ми актуалізували наступні способи складання таблиць множення:
- Спосіб на підставі конкретного змісту дії множення: 2 * 4 = 2 + 2 + 2 + 2 = 8.
- Спосіб на підставі переставної властивості дії множення: 3 * 2 = 2 * 3 = 6.
- Спосіб на підставі попереднього значення: 3 * 7 = 3 * 6 + 3 = 18 + 3 = 21.
- Спосіб на підставі наступного значення: 3 * 9 = 3 * 10 – 3 = 30 – 3 = 27.
- Спосіб групування: 2 * 8 = 2 * 4 + 2 * 4 = 8 + 8 = 16.
Ці способи є також способами запам’ятовування табличних результатів. Складаючи таблицю різними способами ми тим самим працюємо над її запам’ятовуванням: кожний учень для себе відшукує зручний спосіб встановлення результату „важкого” випадку з таблиці.
Розглянемо методику вивчення таблиць множення на прикладі таблиці множення числа 5.
Під час узагальнення і систематизації знань нами було порівняно і з-записано відомі таблиці множення у загальному вигляді: 2 * а, 3 * а, де а приймає значення 2. 3, 4, 5, 6, 7, 8, 9. Використовуючи цей висновок діти можуть самостійно записати добутки, які містить таблиця множення числа 5:
5 * 2
5 * 3
5 * 4
5 * 5
5 * 6
5 * 7
5 * 8
5 * 9
Актуалізувавши переставну властивість дії множення, встановлюємо, що значення окремих добутків нам вже відомі:
5 * 2 = 2 * 5 = 10
5 * 3 = 3 * 5 = 15
5 * 4 = 4 * 5 = 20
Далі з’ясовуємо, якими способами можна знайти значення решти добутків:
1) на підставі конкретного змісту дії множення: 5 * 5 = 5 + 5 + 5 + 5 + 5 = 25;
2) на підставі попереднього значення: 5 * 5 = 5 * 4 + 5 = 20 + 5 = 25;
3) на підставі наступного значення: 5 * 5 = 5 * 6 – 5 = 30 – 5 = 25;
4) на підставі групування: 5 * 6 = 5 * 3 + 5 * 3 = 15 + 15 = 30
Обчисливши значення решти добутків отримуємо повну таблицю множення:
5 * 2 = 10
5 * 3 = 15
5 * 4 = 20
5 * 5 = 25
5 * 6 = 30
5 * 7 = 35
5 * 8 = 40
5 * 9 = 45
З метою запам’ятовування табличних результатів працюємо над готовою таблицею:
- Сформулюйте переставний закон множення. (Від перестановки множників значення добутку не змінюється.)
- Для визначення значень яких добутків ми застосували переставний закон множення?



 5 * 2 = * =
5 * 2 = * =
 | |||||||
 |  |  | |||||
5 * 3 = * =
 |  |  | |||||
 | |||||||
5 * 4 = * =
- Порівняйте попередній і наступний результати з таблиці: 10 та 15, 15 та 20.... Що ви помітили? (Кожний наступний результат на 5 більше попереднього.)
- Чому? (Тому що, в таблиці другий множник кожний раз збільшується на 1. А це означає, що наступна сума містить на одну п’ятірку більше, ніж попередня. Отже, кожний наступний результат на 5 більше попереднього.)
- Використовуючи цю закономірність таблиці множення числа 5, як можна дізнатися про наступний результат? (Треба до попереднього результату додати 5.)
- Наприклад, ви забули скільки буде 5 помножити на 5. (5 * 6, 5 * 7, 5 * 8, 5 * 9) Використовуючи попередній результат, дізнайтеся про наступний результат.
 |  |  |  |  |  |
5 * 5 = * + = + =
 |  |  |  |  |  |
5 * 6 = * + = + =





 5 * 7 = * + = + =
5 * 7 = * + = + =





 5 * 8 = * + = + =
5 * 8 = * + = + =





 5 * 9 = * + = + =
5 * 9 = * + = + =
- На скільки кожний наступний результат більший за попередній? (На 5.)
- Знайдіть значення добутку 5 та 10. Що цікавого ви помітили? (Щоб 5 помножити на 10, треба до п’яти справа приписати один нуль.)
- Наприклад, ви забули скільки буде 5 помножити на 9. (5 * 8, 5 * 7, 5 * 6, 5 * 5) Використовуючи наступний результат відтворіть даний випадок множення.

 5 * 10 =
5 * 10 =
5 * 9 




 = * - = - =
= * - = - =
5 * 8 




 = * - = - =
= * - = - =





 5 * 7 = * - = - =
5 * 7 = * - = - =
5 * 6 




 = * - = - =
= * - = - =
 |  |  |  |  |  |
5 * 5 = * - = - =
- Випадки множення числа 5 на 2, на 3, на 4 ми вже добре знаємо на підставі знання попередніх таблиць і переставної властивості дії множення! Як їх можна використовувати для обчислення інших випадків? (Можна групувати доданки по 2, по 3, по 4 і використовувати оці результати.)
- Групуючи доданки, спробуйте дізнатися про значення наступних добутків:
 |  |  |  |  | |||||||||||||||
 |  |  |  |  | |||||||||||||||
5 * 5 = + + + + = * + * =
 |  |  |  |  |  | ||||||||||||||||
 |  |  |  |  | |||||||||||||||||
5 * 6 = + + + + + = * + * =
 |  |  |  |  |  |  |  |  | |||||||||||||||
 |  |  | |||||||||||||||||||||
5 * 7 = + + + + + + = * + * =
 |  |  |  |  |  |  |  |  |  |  |  |  | |||||||||||||
5 * 8 = + + + + + + + = * + * =
 |  |  |  |  |  |  |  |  | |||||||||||||||||||
 |  |  |  |  |
5 * 9 = + + + + + + + + = * + * =
З метою закріплення таблиці множення числа 5 пропонуємо учням завдання:
1. Запишіть результати з таблиці множення числа 5 в порядку зростання: від найменшого до найбільшого.
2. Запишіть результати з таблиці множення числа 5 в порядку спадання: від найбільшого до найменшого.
3. Запишіть у зошиті по - пам’яті таблицю множення числа 5.
4. Знайдіть значення виразів з таблиці:
5 * 2 = 10
5 * 4 = 20
5 * 6 = 30
5 * 8 = 40
- На які числа множили число 5? (5 множили на 2, 4, 6, 8 – на парні числа.)
- Що можна сказати про значення цих добутків? (Усі добутки подані круглими числами, тобто числами, що закінчуються нулем.)
- Який висновок можна зробити? (При множенні на 2, 4,6, 8 (парні числа) ми отримаємо в добутку число, що закінчується нулем.)
Аналогічно отримуємо інший висновок. При множенні на 3, 5,7, 9 (непарні числа) ми в добутку отримуємо число, що закінчується цифрою 5!
5. Виключіть зайве число: 25, 40, 15, 35, 10, 45, 52, 20, 30.
6. Які випадки з таблиці множення ви добре запам’ятали? П’яти – п’ять – двадцять п’ять! Які випадки з таблиці множення можна відтворити, знаючи про це? (5 * 4 = 5 * 5 – 5 = 25 – 5 = 20, 5 * 6 = 5 * 5 + 5 = 25 + 5 = 30.)
7. Випадок 5 * 9 важко запам’ятати? Як його відтворити? (5 * 10 = 50. 5 * 9 = 5 * 10 – 5 = 50 – 5 = 45.)
8. Які результати ми можемо відтворити на підставі переставної властивості дії множення? (5 * 2 = 2 * 5 = 10, 5 * 3 = 3 * 5 = 15, 5 * 4 = 4 * 5 = 20.)
9. Перша половина таблиці звичайно добре запам’ятовується. Як її можна застосувати для відтворення результатів нижньої частини таблиці? Як можна дізнатися скільки буде, якщо 5 * 6? 5 * 7? 5 * 8?
(5 * 6 = 5 * 5 + 5 = 25 + 5 = 30 або 5 * 6 = 5 * 3 + 5 * 3 = 15 = 15 = 30.
5 * 7 = 5 * 6 + 5 = 30 + 5 = 35 або 5 * 7 = 5 * 3 + 5 * 4 = 15 = 20 = 35.
5 * 8 = 5 * 7 + 5 = 35 + 5 = 40 або 5 * 8 = 5 * 9 – 5 = 45 – 5 = 40 або
5 * 8 = 5 * 4 + 5 * 4 = 20 + 20 = 40.)
10. Доведіть, що 5 * 7 = 35. (5 * 7 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35.)
11. Порівняйте: 5 * 8 та 5 * 6 + 5...
Для контролю заучування таблиці корисні картки типу:
| 1. 5 * 2 = __ 12: 4 = __ 3 * 5 = __ 14: 2 = __ 5 * 7 = __ 4 * 9 = __ 21: 3 = __ 2 * 8 = __ 32: 4 = __ 3 * 6 = __ 5 * 8 = __ 8: 2 = __ 5 * 5 = __ 9: 3 = __ 4 * 5 = __ 20: 2 = __ 1 варіант | __ * 4 = 16 27: __ = 9 2 * __ = 9 __ * 3 = 15 __: 4 = 7 5 * __ = 45 __ * 8 = 24 12: __ = 6 3 * __= 12 __ * 10 = 30 __ * 6 = 30 __: 3 = 4 5 * __ = 20 __: 4 = 10 20: __ = 5 __: 9 = 4 3 * __ = 21 | 2. 5 * 3 = __ 16: 4 = __ 3 * 9 = __ 18: 2 = __ 5 * 9 = __ 4 * 7 = __ 24: 3 = __ 2 * 6 = __ 24: 4 = __ 4 * 3 = __ 5 * 6 = __ 10: 2 = __ 5 * 4 = __ 4 * 10 = __ 30: 3 = __ 6: 2 = __ 2 варіант | 4 * ___ = 32 __ * 7 = 21 5 * __ = 35 16: __ = 8 __: 4 = 9 2 * __ = 20 __ * 2 = 10 18: __ = 6 __ * 4 = 12 5 * __ = 40 __ * 7 = 14 5 * __ = 50 __ * 2 = 4 __ * 5 = 25 __: 2 = 10 4 * __ = 16 __: 3 = 9 |
Як бачимо, перша частина картки спрямована на безпосереднє відтворення табличних результатів, а друга частина – це трансформовані приклади (тут механічне запам’ятовування таблиці не допомагає, тут треба міркувати!).
Таблиці ділення. Таблиця ділення складається на підставі взаємозв’язку між діями множення і ділення: з кожного прикладу на множення можна скласти по два приклади на ділення; але при складанні таблиць нас цікавить лише один приклад. Учні записують в зошитах таблицю множення на певне число, а потім їм пропонується скласти з прикладів на множення приклади на ділення на певне число.
З метою випереджуючого навчання, можна скласти з кожного прикладу на множення по два приклади на ділення:
   5 * 2 = ____________= 5 * 2 = ____________=
5 * 4 =___________=
5 * 6 =____________=
5 * 8 =___________=
5 * 9 =____________=
|   10: 5 =, т.к. * 5 = 10 10: 5 =, т.к. * 5 = 10
  * *
|   10: 2 =, т.к. * 2 = 10 10: 2 =, т.к. * 2 = 10
  * *
  15: 3 =, т.к. * 3 = 15 15: 3 =, т.к. * 3 = 15
  * *
|
При складанні таблиці ділення, можна міркувати ще й так: 15: 5 – це означає знайти таке число, яке при множенні на 5 дає 15 – це число 3.
Результати навчання повинні контролюватися з боку вчителя. Діагностувати, як учень володіє вивченими випадками таблиць множення і ділення можна за допомогою карток типу:
| 5 * 6 = __ 32: 4 = __ 3 * 9 = __ 16: 2 = __ 40: 5 = __ 4 * 7 = __ 18: 3 = __ 2 * 6 = __ 5 * 4 = __ 24: 4 = __ 3 * 7 = ___ 10: 2 = __ 25: 5 = __ 1 варіант | 5 * 9 = __ 36: 4 = __ 3 * 8 = __ 14: 2 = __ 5 * 7 = __ 16: 4 = __ 24: 3 = __ 15: 5 = __ 12: 4 = __ __ * 2 = 10 20: __ = 5 __: 3 = 4 __ * 3 = 15 2 * __ = 18 | 4 * 4 = __ 25: 5 = __ 24: 3 = __ 2 * 8 = __ 5 * 6 = __ 32: 4 = __ 3 * 6 = __ 12: 2 = __ 40: 5 = __ 4 * 7 = __ 21: 3 = __ 2 * 7 = __ 5 * 4 = __ 2 варіант | 24: 4 = __ 15: 3 = __ 2 * 9 = __ 5 * 9 = __ 36: 4 = __ 3 * 9 = __ 10: 2 = __ 35: 5 = __ 4 * __ = 20 12: __ = 4 __ * 3 = 9 __: 5 = 3 12: __ = 3 __ * 2 = 20 |
Методика вивчення нумерації трицифрових чисел.
Вимоги до знань, умінь і навичок:
- Знати назви чисел в межах 1000 і порядок їх прямування в натуральному ряді. Вміти рахувати, починаючи з будь-якого числа, в прямому і зворотному порядку.
- Знати місце кожного числа від 1 до 1000, вміти назвати його сусідів, попереднє та наступне число.
- Знати назви трьох розрядів: 1 розряд – розряд одиниць, П розряд – розряд десятків, Ш розряд – розряд сотень. Засвоїти, що 10 одиниць нижчого розряду складають 1 одиницю вищого розряду.
- Вміти утворювати трицифрові числа із сотень, десятків та одиниць, а також прирахуванням по 1 та відрахуванням по 1.
- Знати,які числа називаються трицифровими і вживати термін “трицифрове” число.
- Вміти читати і записувати трицифрові числа, усвідомлюючи значення кожної цифри в запису числа.
- Вміти подавати будь-яке число у вигляді суми розрядних доданків.
- Вміти визначати в числі загальну кількість одиниць, десятків сотень.
- Вміти порівнювати числа за місцем на в натуральному ряді та, використовуючи десятковий склад числа – порозрядне порівняння.
- Вміти виконувати арифметичні дії додавання і віднімання на підставі знань з нумерації:
- порядку прямування чисел в натуральному ряді: 453 + 1, 453 – 1;
- десяткового складу чисел: 500 + 40, 500 + 40 + 7, 500 + 7; 567 – 500, 567 – 60, 567 – 7.
Наочні посібники і дидактичний матеріал:
- палички, пучки-десятки, пучки-сотні;
- абак;
- таблиця розрядів і класів.
Формуємо поняття про сотню, як про складену лічильну одиницю. В концентрі “Сотня” діти познайомилися з двома лічильними одиницями – одиницею і складеною лічильною одиницею – десятком. 10 окремих паличок - одиниць зв’язували в пучок – десяток, далі пучки-десятки рахували так само, як і прості одиниці.
Аналогічно здійснюється ознайомлення з новою лічильною одиницею – сотнею. 10 паличок зв’язують в пучок і кажуть – 1 десяток, записуємо:
10 одиниць = 1 десятку.
Лічимо пучками-десятками. Отримав 10 десятків, зв’язуємо їх у великий пучок – сотню, записуємо: 10 десятків = 1 сотні
Звертаємо увагу, що отримана нова лічильна одиниця називається сотнею, і пропонуємо учням здогадатися, чому саме вона так називається. В 1 десятку 10 одиниць, а в 10 десятках 100 одиниць, або сотня. Записуємо:
100 одиниць = 1 сотні.
Далі вчитель запитує, чи не можна рахувати пучками – сотнями, так як рахували простими одиницями або десятками. Потім учні рахують сотнями: 1 сотня, 2 сотні... до 10 сотень.
Вчитель повідомляє, що 10 сотень складають 1 тисячу і записує це на дошці:
|
Для наочної інтерпретації можна скористатися посібником “Риски та квадрати”:
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На підставі аналогії вводяться назви чисел третього розряду:

Учні переходять до назв: 2 сотні – дві-сті; 3 сотні – три-ста... Назви цих чисел діляться на дві частини, при чому перша частина слова вказує кількість сотень, а друга частина слова, вказує що рахують сотнями.
Після того, як діти навчаться рахувати сотнями (називати не лише 2 сотні але й двісті) до тисячі, а також визначати скільки одиниць, десятків в одній чи кількох сотня, учні вчаться у утворювати числа із 1 сотні і кількох одиниць: сто один... сто дев’ять, сто десять. Потім, на підставі порівняння утворення чисел з кількох десятків і кількох одиниць, діти вчаться утворювати числа з однієї сотні, кількох десятків і кількох одиниць:
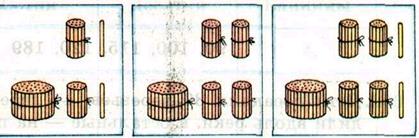
Далі школярі знайомляться з новим розрядом “сотні” і вчаться читати числа, записані в нумераційній таблиці. З’ясовують, скільки сотень, десятків та одиниць в кожному числі. Серед чисел пропонується число 101, в середині запису якого є нуль, тому що воно містить 0 десятків. Це одне з чисел, яке викликає певні труднощі у дітей при записі.
Також треба узагальнити спосіб отримання чисел першої сотні прирахування одиниці до попереднього та відрахування по одиниці із наступного числа. Застосовуються терміни попереднє та наступне число. На цій підставі розглядаються випадки додавання 1, в межах першої сотні.
Трохи пізніше учні вчаться рахувати, при чому пропонуються такі завдання, щоб обов’язково був перехід через розряд: від 95 до 105, від 157 до 165; подавати числа першої сотні у вигляді суми розрядних доданків: 138 = 100 + 30 + 8.
Спочатку діти подають двоцифрове число у вигляді суми десятків та одиниць: 83 = 80 + 3, з’ясовують чому ця сума містить два доданки (тому що число 83 – двоцифрове і містить два розряди.) Таким чином, двоцифрове число подається у вигляді суми двох розрядних доданків, де окремо подані десятки і окремо подані одиниці. Виходячи з цього, скільки ж розрядних доданків містить трицифрове число? (Трицифрове число розкладається на суму трьох розрядних доданків, тому що воно містить три розряди: сотні, десятки та одиниці.) Сума, в якій окремо подані одиниці кожного розряду: сотні, десятки та одиниці, називається сумою розрядних доданків.
Далі пропонується обернене завдання записати число, яке подано сумою розрядних доданків: 100 + 30 + 5 = 135.
В подальшому навчанні учні утворюють трицифрові числа із сотень, десятків та одиниць. Учні виконують вправи,як в утворенні чисел із кількох сотень, кількох десятків та кількох одиниць, а також виконують обернені вправи: називають скільки в даному числі сотень, десятків та одиниць. Вправи виконуються спочатку з застосуванням наочних посібників (паличок і пучків паличок: десятків і сотень; або рисок та квадратів). Наприклад:
Вправа: покладіть на парти 2 маленьких квадратика (одиниці), 5 рисок (десятків) і 4 великих квадрати (сотні). Назвіть це число (452). Скільки в ньому одиниць, скільки десятків, скільки сотень (4 сотні, 5 десятків, 2 одиниці).
Без наочних посібників аналогічна вправа звучить наступним чином: скільки сотень, десятків та одиниць в числі 957. Назвіть число, в якому 3 сотні, 2 десятки і 7 одиниць.
Найбільші труднощі уявляють числа, в яких відсутні одиниці або десятки, тому доцільні вправи:
- визначити на слух склад числа 560, 506 й тощо;
- назвати числа,, в яких 7 сотень і 2 одиниці й тощо.
Далі вводиться поняттям про розряди: “1 розряд”, “П розряд”, “Ш розряд”, узагальнюються назви чисел кожного розряду:
| Ш розряд | П розряд | 1 розряд |
| сто | десять | один |
| двісті | двадцять | два |
| триста | тридцять | три |
| чотириста | сорок | чотири |
| п’ятисот | п’ятдесят | п’ять |
| шістсот | шістдесят | шість |
| сімсот | сімдесят | сім |
| вісімсот | вісімдесят | вісім |
| Дев’ятисот | дев’яносто | дев’ять |
Таким чином, одиниці – називаються одиницями 1 –го розряду, десятки – одиницями П-го розряду, сотні – одиницями – Ш-го розряду.
Порівняння трицифрових чисел відбувається двома способами. Наприклад, треба порівняти число 235 та 236: число 235 при рахунку йде раніше, ніж число 236, тому 235< 236 – це спосіб порівняння на підставі прямування чисел в натуральному ряді.
Другий спосіб порівняння чисел – порозрядне порівняння. Наприклад, треба порівняти 205 та 250: порівняння починаємо з найвищого розряду сотень – в першому числі 2 сотні і в другому числі 2 сотні, сотень порівну, переходимо до розряду десятків – в першому числі 0 десятків, а в другому 5 десятків, 0 < 5, тому 205 < 250.
Запис трицифрових чисел спочатку здійснюється в нумераційній таблиці. Спочатку пропонуємо числа вже з визначеним десятковим складом: 5 сотень, 2 десятки та 7 одиниць; а потім подаються лише назви чисел, а десятковий склад учні повинні визначити самі. Можна пропонувати спочатку записувати числа в нумераційній таблиці, а потім без неї.
Далі, на підставі аналогії з додаванням одиниць і круглих десятків, учні вчаться додавати і віднімати розрядні числа – круглі сотні. Тут застосовується спосіб укрупнення розрядних одиниць:
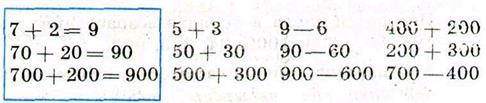
|
Наприклад, 700 – 400.
- Замінюю кожне число сотнями: 7 сот. – 4 сот.
- Віднімаю числа сотень: 7 сот. – 4 сот. = 3 сот.
- Результат подаю в одиницях: 3 сот. = 300.
700 – 400 = 7 сот. – 4 сот. = 3 сот.= 300
Розкладати трицифрові числа на розрядні доданки учні вже вміють, тому далі вони виконують обернені завдання - замінюють суму розрядних доданків трицифровим числом. При заміні суми розрядних доданків трицифровим числом учні міркують так:
600 + 30 + 1
- 600 – це 6 сотень, 30 – це 3 десятки, 1 – 1 одиниці.
- Число, що містить 6 сотень, 3 десятки та 1 одиницю – це число 631
Учні вчаться встановлювати, що означає кожна цифра в запису числа, скільки в даному числі одиниць кожного розряду.
Наприклад, в числі 627, цифра 7 означає число одиниць, цифра 2 означає число десятків, а цифра 6 – число сотень. В числі 627 в третьому розряді 6 одиниць, або 6 сотень, в другому розряді – 2 одиниці або 2 десятки, а в першому – 7 одиниць.
Навчання встановленню загальної кількості десятків, сотень і одиниць в числі відбувається на підставі розгляду вправ:
| 60 = 6 дес. | В числі 60 всього 6 десятків |
| 200 = 20 дес. | В числі 200 всього 20 десятків |
| 260 = 26 дес. | В числі 260 всього 26 десятків. |
Для того, щоб дізнатися про загальну кількість десятків в числі, треба закрити в ньому 1 цифру справа.
| Число | Всього | ||
| сотень | десятків | одиниць | |
Для того, щоб дізнатися загальне число сотень в числі, треба справа закрити 2 цифри.
Далі учні знайомляться з випадками віднімання на підставі десяткового складу числа: 345 – 300, 345 – 40, 345 – 5.
|
Наприклад, 853 – 50:
- 853 – це 8 сотень, 5десятків та 3 одиниці;
- 50 – це 5 десятків.
- Було 8 сотень 5 десятків та 3 одиниці, відняли 5 десятків, отримали 8 сотень і 3 одиниці – це число 803.
-
 853 – 50 = 803.
853 – 50 = 803.
Знання з нумерації чисел в межах 1000 закріплюються і систематизуються при вивченні теми “Міри довжини і маси”.
Методика вивчення додавання і віднімання в межах 1000.















 числа розрядних одиниць.
числа розрядних одиниць. .
. .
. ”, “Отримали”.
”, “Отримали”.
