
Відповідь: а = 1,65 м/c2.
Приклад 4 На похилій площині, що утворює з горизонтом кут  , знаходиться тіло масою
, знаходиться тіло масою  = 2 кг (рис. 5). Тіло рухається вгору по похилій площині під дією зв'язаного з ним невагомою і нерозтяжною ниткою, перекинутою через блок, вантажу масою
= 2 кг (рис. 5). Тіло рухається вгору по похилій площині під дією зв'язаного з ним невагомою і нерозтяжною ниткою, перекинутою через блок, вантажу масою  = 20 кг. Початкові швидкості тіла і вантажу дорівнюють нулю, коефіцієнт тертя тіла
= 20 кг. Початкові швидкості тіла і вантажу дорівнюють нулю, коефіцієнт тертя тіла  = 0,1. Визначити прискорення, з яким рухаються тіла, і силу натягу нитки. Блок вважати невагомим, тертям знехтувати.
= 0,1. Визначити прискорення, з яким рухаються тіла, і силу натягу нитки. Блок вважати невагомим, тертям знехтувати.
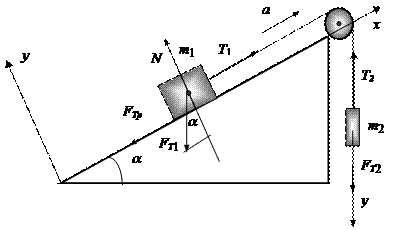 |
исунок 5 - Тіло на похилій площині
Розв'язання. На тіло  , яке рухається по похилій площині, діє сила тяжіння
, яке рухається по похилій площині, діє сила тяжіння  , сила натягу нитки
, сила натягу нитки  , сила
, сила
тертя 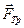 і сила реакції опори
і сила реакції опори 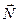 . На вантаж
. На вантаж  діє сила тяжіння
діє сила тяжіння 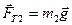 і сила натягу нитки
і сила натягу нитки  . Тут
. Тут 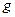 – прискорення вільного падіння. Другий закон Ньютона (рівняння руху) для цих тіл буде мати вигляд
– прискорення вільного падіння. Другий закон Ньютона (рівняння руху) для цих тіл буде мати вигляд
 , (12)
, (12)
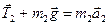 , (13)
, (13)
де  ,
,  - прискорення руху тіл.
- прискорення руху тіл.
Із умови невагомості і нерозтяжності нитки та відсутності тертя випливає, що  ,
,  .
.
Виберемо для тіла 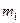 систему відліку хОу так, як показано на рисунку 5. Тоді рівняння руху цього тіла в проекціях на осі х і у запишеться так
систему відліку хОу так, як показано на рисунку 5. Тоді рівняння руху цього тіла в проекціях на осі х і у запишеться так
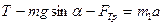 , (14)
, (14)
 . (15)
. (15)
Із співвідношення (15) знайдемо  та підставимо у рівняння (14), врахувавши, що
та підставимо у рівняння (14), врахувавши, що 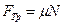 , тоді отримаємо
, тоді отримаємо
 , (16)
, (16)
де  - коефіцієнт тертя.
- коефіцієнт тертя.
Рівняння руху вантажу  у проекції на вертикальну вісь
у проекції на вертикальну вісь 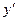 має вигляд
має вигляд
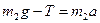 . (17)
. (17)
Розв'язавши систему рівнянь (16) та (17) відносно а, після простих перетворень отримаємо
 . (18)
. (18)
Знаючи а, підставивши співвідношення (18) у вираз (17) знайдемо силу натягу нитки
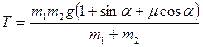 .
.
Після підстановки числових значень фізичних величин отримаємо
 м/c2,
м/c2,
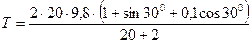 =28,2 Н.
=28,2 Н.
Перевіримо розмірності отриманих величин
 ,
,
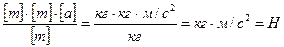 .
.
Відповідь:  8,4 м/c2,
8,4 м/c2, 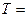 28,2 Н.
28,2 Н.
Приклад 5 По дотичній до шківа маховика у вигляді диска діаметром D = 75 см і масою m = 40 кг прикладена сила F =1 кН (рис.6). Визначити кутове прискорення  і частоту обертання n маховика через час t = 10 c після початку дії сили, якщо відстань, на якій прикладається сила (радіус шківа) дорівнює r = 12 см. Силою тертя знехтувати.
і частоту обертання n маховика через час t = 10 c після початку дії сили, якщо відстань, на якій прикладається сила (радіус шківа) дорівнює r = 12 см. Силою тертя знехтувати.
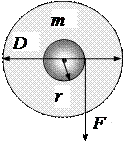 |
Рисунок 6 – Обертання маховика під дією сили
Розв’язання. Запишемо для маховика основне рівняння динаміки обертального руху
M = Je, Þ e = 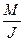 , (19)
, (19)
де e - кутове прискорення маховика; І – момент інерції; М – момент прикладеної сили.
Момент інерції диска дорівнює
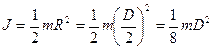 , (20)
, (20)
де  – радіус диска;
– радіус диска; 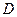 - його діаметр.
- його діаметр.
Момент сили F знайдемо зі співвідношення
М=Fd =Fr, (21)
де d – плече сили.
Підставивши співвідношення (20), (21) в (19), отримаємо
 . (22)
. (22)
Рух під дією сталої сили є рівноприскореним. Звідси кутова швидкість диска
 .
.
За визначенням w=2pn, де  - частота обертання диска. У результаті отримаємо
- частота обертання диска. У результаті отримаємо
 ,
,
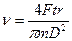 . (23)
. (23)
Підставивши числові значення величин у співвідношення (22), (23), знайдемо остаточно
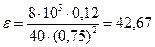 рад/с2,
рад/с2,
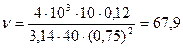 с-1.
с-1.
Перевіримо розмірності отриманих величин
 ,
,
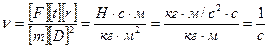 .
.
Відповідь: e = 42,67 рад/с2; n = 67,9 с-1.
Приклад 6 Блок, що має форму диска масою m = 0,4 кг, обертається під дією сили натягу нитки, до кінців якої підвішені тягарці масами m1 = 0,3 кг і m2 = 0,7 кг (рис.7). Визначити сили натягу T1 і T2 нитки з обох сторін блока.
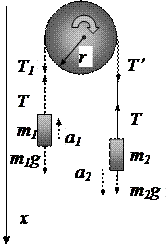 |
Рисунок 7 – Рух зв’язаних тіл під дією сил
Розв’язання. Для розв’язання задачі скористаємося рівняннями обертального і поступального руху тіл. Оскільки m2>m1, то m2g>T2. Рівнодійна сил тяжіння і натягу нитки викликає рівноприскорений рух системи, при цьому обертання блока здійснюється за годинниковою стрілкою (рис.7). Для тіл, що рухаються поступально, можна записати другий закон Ньютона:
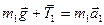 ,
,

де 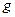 - прискорення вільного падіння.
- прискорення вільного падіння.
У проекціях на вісь x ці рівняння будуть мати вигляд

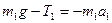 , (24)
, (24)
х
 , (25)
, (25)
де 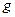 - прискорення вільного падіння.
- прискорення вільного падіння.
Згідно з основним рівнянням обертального руху, для блока отримаємо вираз
 , (26)
, (26)
де М – момент сил, прикладених до блока; J – момент інерції блока; e - кутове прискорення блока.
Визначимо обертальний момент сил. Врахуємо при цьому, що прискорення вантажів однакові  . Сили натягу ниток діють не тільки на вантажі, але й на диск. За третім законом Ньютона сили
. Сили натягу ниток діють не тільки на вантажі, але й на диск. За третім законом Ньютона сили 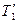 і
і 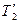 , що прикладені до блока, дорівнюють відповідно силам Т1 і Т2, але за напрямком протилежні їм. При русі вантажів блок прискорено обертається за годинниковою стрілкою, отже,
, що прикладені до блока, дорівнюють відповідно силам Т1 і Т2, але за напрямком протилежні їм. При русі вантажів блок прискорено обертається за годинниковою стрілкою, отже, 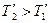 . Для обертального моменту сил, що прикладені до блока, можна записати:
. Для обертального моменту сил, що прикладені до блока, можна записати:
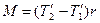 . (27)
. (27)
Кутове прискорення блока пов’язане з лінійним прискоренням вантажів співвідношенням
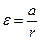 . (28)
. (28)
Підставивши вирази (26) та (28) у (27), отримаємо
 . (29)
. (29)
Момент інерції блока дорівнює
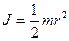 . (30)
. (30)
Тоді
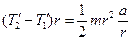 .
.
Після скорочення отримаємо
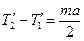 . (31)
. (31)
Враховуючи, що 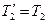 , а
, а 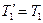 , одержимо
, одержимо
 . (32)
. (32)
Розв’яжемо спільно систему трьох рівнянь (24), (25) і (32). З рівняння (24) а дорівнює
 . (33)
. (33)
Підставивши це рівняння у (25), отримаємо

або
 . (34)
. (34)
Підставивши дане рівняння у (32), знайдемо
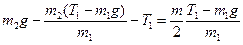 . (35)
. (35)
Після ряду перетворень співвідношення (35) визначимо T1
 ,
,
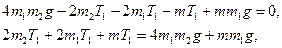
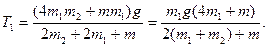 (36)
(36)
Підставивши даний вираз у (34), отримаємо
 . (37)
. (37)
Після підстановки числових значень величин у співвідношення (36) та (37), отримаємо кінцевий результат
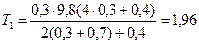 Н,
Н,
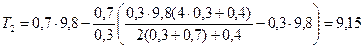 Н.
Н.
Зрозуміло, що одиниця вимірювання отриманих величин - ньютон.
Відповідь: Т 1=1,96 Н; Т2 =9,15 Н.
Приклад 7 Човен довжиною  =3 м і масою
=3 м і масою 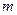 =120 кг стоїть на спокійній воді. На носі і кормі знаходяться два рибалки масою
=120 кг стоїть на спокійній воді. На носі і кормі знаходяться два рибалки масою 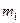 =60 кг і
=60 кг і  =90 кг (рис.8). На скільки зміститься човен відносно води, якщо рибалки поміняються місцями?
=90 кг (рис.8). На скільки зміститься човен відносно води, якщо рибалки поміняються місцями?
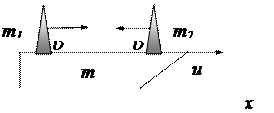
Розв’язання. Запишемо закон збереження імпульсу для механічної системи „рибалки-човен”. Врахуємо, що в початковий момент часу система знаходилась у стані спокою, а при русі рибалок зі швидкістю u відносно човна почнеться його
рух зі швидкістю u відносно дна озера. У вибраній системі
 | |||
 |
Рисунок 8 – Зміщення човна при русі рибалок
відліку(відносно землі) закон збереження імпульсу має вигляд
 . (38)
. (38)
У проекції на вісь х співвідношення (38) запишеться так
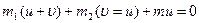 .
.
Розв’яжемо це рівняння відносно u:
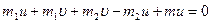 ,
,
 ,
,
 ,
,
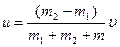 .
.
Помноживши обидві частини цього рівняння на час руху t, визначимо зміщення човна
 ,
,
але 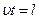 ;
;  .
.
Звідси
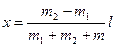 . (39)
. (39)
Після підстановки числових значень величин у співвідношення (39) знайдемо х
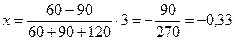 м.
м.
Знак мінус свідчить про те, що переміщення відбулося в напрямку, протилежному напрямку осі x.
Відповідь: х = 0,33 м.
Приклад 8 Куля масою 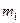 =1 кг рухається зі швидкістю
=1 кг рухається зі швидкістю  =4 м/с і зіштовхується з кулею масою
=4 м/с і зіштовхується з кулею масою  =2 кг, що рухається назустріч їй зі швидкістю
=2 кг, що рухається назустріч їй зі швидкістю 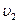 =3 м/с (рис.9). Які швидкості
=3 м/с (рис.9). Які швидкості  і
і  куль після удару? Удар вважати абсолютно пружним, прямим, центральним.
куль після удару? Удар вважати абсолютно пружним, прямим, центральним.
 |
Рисунок 9 – Швидкості куль до та після пружного удару
Розв’язання. При пружному центральному ударі справедливі закони збереження імпульсу і механічної енергії. Запишемо їх для даної системи:
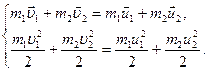 (40)
(40)
Спроектуємо рівняння (40) на вісь х
 (41)
(41)
Розв’яжемо спільно систему рівнянь (41)
 (42)
(42)
 (43)
(43)
Розділивши друге співвідношення на перше, отримаємо таку систему рівнянь
 . (44)
. (44)
Визначивши u1 з першого рівняння і підставивши його у друге, одержимо
 . (45)
. (45)
Після ряду перетворень співвідношень (45) знайдемо u2:
 ,
,
 ,
,
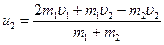 . (46)
. (46)
Підставивши дане рівняння у (45), отримаємо
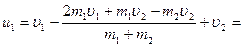
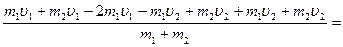
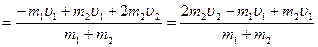 . (47)
. (47)
Підставивши числові значення величин у вирази (46) та (47), отримаємо відповідь
 м/с,
м/с,
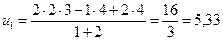 м/с.
м/с.
Видно, що одиниця вимірювання отриманих величин - м/с.
Відповідь: u 1 = 5,33 м/с; u 2 = 1,67 м/с.
Приклад 9 По горизонтальній площині котиться диск зі швидкістю 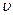 = 8 м/c (рис.10). Визначити коефіцієнт опору, якщо диск зупинився, пройшовши шлях S = 18 м.
= 8 м/c (рис.10). Визначити коефіцієнт опору, якщо диск зупинився, пройшовши шлях S = 18 м.
 |
Рисунок 10 – Рух диска під дією сили тертя
Розв’язання. Для розв’язання задачі скористаємось законом збереження енергії. У точці А (рис.10) тіло має кінетичну енергію Ek, яка складається з енергії поступального та обертального руху. У точці В ця енергія дорівнює 0. Кінетична енергія витрачається на виконання роботи проти неконсервативних сил (сили тертя 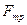 )
)
 , (48)
, (48)
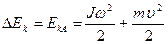 , (49)
, (49)
де 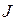 - момент інерції диска;
- момент інерції диска;  - його кутова швидкість.
- його кутова швидкість.
Робота, що здійснюється тілом, дорівнює
А=-FS=-mmgS, (50)
де  - коефіцієнт тертя.
- коефіцієнт тертя.
Підставивши співвідношення (49) і (50) в (48), отримаємо
 . (51)
. (51)
Для диска момент інерції дорівнює
 , (52)
, (52)
де  - радіус диска.
- радіус диска.
Кутову швидкість обертання диска знайдемо із співвідношення
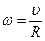 . (53)
. (53)
Звідси, підставивши вирази (31) і (32) у (30), отримаємо
 . (54)
. (54)
Після ряду перетворень це співвідношення набуде вигляду
 . (55)
. (55)
Із виразу (55) знайдемо m:
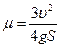 . (56)
. (56)
Після підстановки числових значень величин у (56) отримаємо
 .
.
Перевіримо одиниці отриманої величини
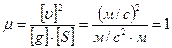 .
.
Відповідь: m = 0,27.
Приклад 10 Платформа у вигляді суцільного диска радіусом R =1,5 м і масою 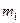 =180 кг обертається навколо вертикальної осі з частотою n =10 хв-1. У центрі платформи стоїть людина масою
=180 кг обертається навколо вертикальної осі з частотою n =10 хв-1. У центрі платформи стоїть людина масою  = 60 кг. Яку лінійну швидкість
= 60 кг. Яку лінійну швидкість  відносно підлоги приміщення матиме людина, якщо вона перейде на край платформи (рис.11)?
відносно підлоги приміщення матиме людина, якщо вона перейде на край платформи (рис.11)?
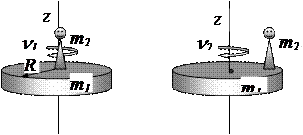 |
Рисунок 11 – Рух системи платформа-людина до і після переміщення людини
Розв’язання. Згідно з умовою задачі, момент зовнішніх сил відносно осі обертання z, що збігається з геометричною віссю платформи, можна вважати таким, що дорівнює нулю. За цієї умови проекція  моменту імпульсу системи платформа - людина залишається сталою:
моменту імпульсу системи платформа - людина залишається сталою:
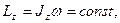 (57)
(57)
де 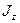 - момент інерції платформи з людиною відносно осі z;
- момент інерції платформи з людиною відносно осі z;  - кутова швидкість платформи.
- кутова швидкість платформи.
Момент інерції системи дорівнює сумі моментів інерції тіл, що входять до складу системи, тому в початковому стані 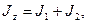 а в кінцевому стані
а в кінцевому стані 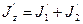 .
.
З урахуванням цього співвідношення (57) набуде вигляду
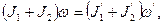 (58)
(58)
де значення моментів інерції  і
і 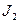 платформи і людини відповідно відносяться до початкового стану системи;
платформи і людини відповідно відносяться до початкового стану системи; 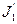 і
і 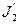 - до кінцевого.
- до кінцевого.
Момент інерції платформи відносно осі z під час переходу людини не змінюється: 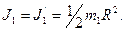 Момент інерції людини відносно тієї самої осі буде змінюватися. Якщо розглядати людину як матеріальну точку, то її момент інерції
Момент інерції людини відносно тієї самої осі буде змінюватися. Якщо розглядати людину як матеріальну точку, то її момент інерції 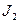 в початковому стані (в центрі платформи) можна вважати таким, що дорівнює нулю. В кінцевому стані (на краю платформи) момент інерції людини дорівнює
в початковому стані (в центрі платформи) можна вважати таким, що дорівнює нулю. В кінцевому стані (на краю платформи) момент інерції людини дорівнює 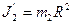 . Врахуємо, що
. Врахуємо, що 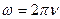 , а
, а  , де
, де  - частота обертання платформи;
- частота обертання платформи; 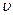 - швидкість людини відносно підлоги.
- швидкість людини відносно підлоги.
Підставимо у формулу (58) вирази для моментів інерції, початкової кутової швидкості обертання платформи з людиною і кінцевої кутової швидкості:

Після скорочення на 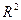 і простих перетворень знаходимо швидкість
і простих перетворень знаходимо швидкість
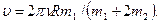 (59)
(59)
Після підстановки числових значень фізичних величин у співвідношення (59) проведемо обчислення
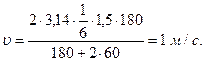
Перевіримо розмірність отриманої величини
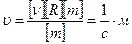 .
.
Відповідь: 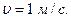
Приклад 11 На лаві Жуковського стоїть людина і тримає в руках стрижень вертикально вздовж осі лави. Лава з людиною обертається з кутовою швидкістю w1 = 4 рад/с (рис.12). З якою швидкістю w2 почне обертатися лава, якщо людина поверне стрижень так, що він набуде горизонтального положення. Сумарний момент інерції людини і лави J = 5 кг×м2. Довжина стрижня l = 1,8 м, його маса m = 6 кг. Вважати, що центр мас стрижня з людиною знаходиться на осі платформи.
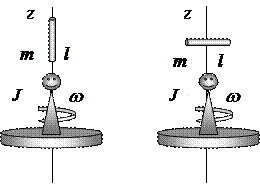 |
Рисунок 12 – Рух системи платформа-людина до і після зміни положення стрижня
Розв’язання. Для розв’язання задачі скористаємося законом збереження моменту імпульсу відносно осі z, навколо якої відбувається обертання:
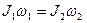 , (60)
, (60)
де J1 та J2 – моменти інерції системи в початковий та кінцевий моменти часу; w1, w2 – відповідні кутові швидкості.
Момент інерції системи дорівнює сумі моментів інерції тіл, що входять в систему:
J1=J+J1′, (61)
J2=J+ J2′, (62)
де J, J1′, J2 – моменти інерції людини та лави до та після повороту стрижня.
Врахуємо, що
J1¢= 0; J2¢= 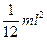 . (63)
. (63)
Після підстановки виразів (61) - (63) в (60) отримаємо
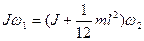 .
.
Звідси
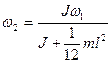 . (64)
. (64)
Після підстановки числових значень фізичних величин у співвідношення (64) знайдемо
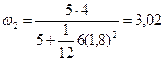 рад/с.
рад/с.
Видно, що одиниця отриманої величини - рад/с.
Відповідь: w2 =3,02 рад/с.
Приклад 12 Однорідний стрижень довжиною  м і масою M = 0,7 кг підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. В точку, що знаходиться на відстані
м і масою M = 0,7 кг підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. В точку, що знаходиться на відстані 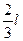 , абсолютно пружно вдаряє куля масою
, абсолютно пружно вдаряє куля масою  г, що летить перпендикулярно до стрижня і його осі. Після удару стрижень відхилився на кут
г, що летить перпендикулярно до стрижня і його осі. Після удару стрижень відхилився на кут 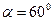 (рис.13). Визначити швидкість кулі.
(рис.13). Визначити швидкість кулі.
Розв’язання. Запишемо закон збереження моменту імпульсу для системи „куля-стрижень”. Оскільки  і удар абсолютно пружний, будемо вважати, що швидкість кулі до
і удар абсолютно пружний, будемо вважати, що швидкість кулі до 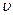 і після удару
і після удару 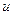 однакова за модулем. Тоді можна записати
однакова за модулем. Тоді можна записати
 |
Рисунок 13 – Взаємодія стрижня з кулею
 , (65)
, (65)
де  – кутова швидкість стрижня;
– кутова швидкість стрижня; 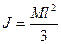 - його момент інерції відносно точки О.
- його момент інерції відносно точки О.
З урахуванням того, що  , співвідношення набуде вигляду
, співвідношення набуде вигляду
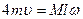 . (66)
. (66)
Скористаємося законом збереження енергії. У нижній точці стрижень має кінетичну енергію, у верхній – потенціальну, тобто:
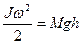 . (67)
. (67)
З рисунка видно, що
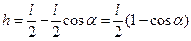 . (68)
. (68)
Підставивши даний вираз у (62), отримаємо
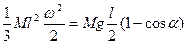
або після скорочення та простих перетворень
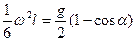 ,
,
 ,
,
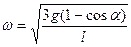 . (69)
. (69)
Підставимо рівняння (69) в (66) і розв’яжемо отримане співвідношення відносно 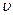 :
:
 (70)
(70)
Підставивши в рівняння (70) числові значення величин, отримаємо кінцевий результат
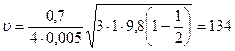 м/с.
м/с.
Перевіримо розмірність отриманої величини
 .
.
Відповідь: u = 134 м/с.
Приклад 13 У балоні об’ємом V =10 л знаходиться гелій під тиском 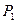 - 1 МПа при температурі
- 1 МПа при температурі 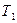 = 300 К. Після того як з балона було узято m = 10 г гелію, температура в балоні знизилася до
= 300 К. Після того як з балона було узято m = 10 г гелію, температура в балоні знизилася до 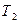 = 290 К. Визначити тиск
= 290 К. Визначити тиск 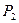 гелію, що залишився в балоні.
гелію, що залишився в балоні.
Розв’язання. Для розв’язання задачі скористаємося рівнянням Менделєєва-Клапейрона, застосувавши його до кінцевого стану газу:
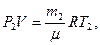 (71)
(71)
де  - маса гелію в балоні в кінцевому стані;
- маса гелію в балоні в кінцевому стані;  - молярна маса гелію; R - молярна газова стала.
- молярна маса гелію; R - молярна газова стала.
З рівняння (71) знайдемо тиск газу
 (72)
(72)
Масу  гелію визначимо через масу
гелію визначимо через масу 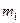 , що відповідає його початковому стану, і масу m гелію, узятого з балона:
, що відповідає його початковому стану, і масу m гелію, узятого з балона:
 . (73)
. (73)
Масу 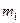 гелію також знайдемо з рівняння Менделєєва - Клапейрона, застосувавши його до початкового стану газу
гелію також знайдемо з рівняння Менделєєва - Клапейрона, застосувавши його до початкового стану газу
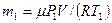 . (74)
. (74)
Підставивши вираз маси 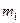 в (73), а потім вираз
в (73), а потім вираз  в (72), знайдемо
в (72), знайдемо

або
 (75)
(75)
Після підстановки числових значень фізичних величин отримаємо
 Па.
Па.
Перевіримо розмірність одержаної величини. Для цього в праву частину виразу замість символів величин підставимо їх одиниці. У правій частині співвідношення маємо два доданки. Очевидно, що перший із них дає одиницю тиску, оскільки складається з двох множників, перший з яких ((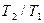 ) – безрозмірний, а другий – тиск. Перевіримо другий доданок:
) – безрозмірний, а другий – тиск. Перевіримо другий доданок:
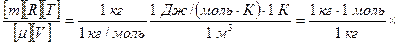
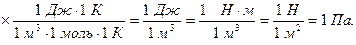
Відповідь: 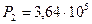 Па.
Па.
Приклад 14 При адіабатичному стисканні тиск повітря збільшився від P1 = 50 кПа до P2 = 0,5 МПа. Потім при незмінному об’ємі температура повітря була знижена до початкової (рис.14). Визначити тиск газу P3 у кінці процесу.
Розв’язання. У випадку адіабатного процесу параметри системи змінюються у відповідності до рівняння
 , (76)
, (76)
де 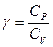 - стала Пуассона.
- стала Пуассона.

Рисунок 14 – Зміна параметрів газу при термодинамічному процесі
Теплоємності при сталому тиску СP і об’ємі СV дорівнюють у випадку двохатомного газу(і =5)
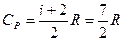 , (77)
, (77)
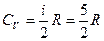 , (78)
, (78)
де i – число ступенів вільності молекули газу; R - газова стала.
Звідси 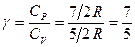 .
.
Другий процес є ізохорним, у цьому випадку
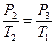 Þ
Þ 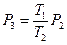 . (79)
. (79)
Рівняння (76) перепишемо з використанням закону Менделєєва-Клапейрона
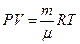 ,
,
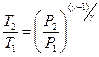 . (80)
. (80)
Підставивши вираз (80) в (79), отримаємо
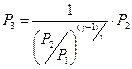 . (81)
. (81)
Підставивши в дане співвідношення числові значення фізичних величин, отримаємо
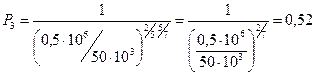 Па.
Па.
Видно, що отримана величина має розмірність - Па.
Відповідь: Р3 =0,52 Па.
Приклад 15 Визначити роботу  , яку виконує азот, якщо йому при сталому тиску надати кількість теплоти
, яку виконує азот, якщо йому при сталому тиску надати кількість теплоти 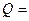 =21 кДж. Знайти також зміну
=21 кДж. Знайти також зміну  внутрішньої енергії газу.
внутрішньої енергії газу.
Розв’язання. У випадку ізобаричного процесу P =const перший закон термодинаміки має вигляд
 .
.
Кількість теплоти, робота газу та його внутрішня енергія визначаються за формулами:
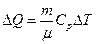 , (82)
, (82)
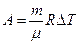 , (83)
, (83)
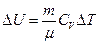 , (84)
, (84)
де R - газова стала; 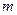 - маса газу;
- маса газу;  - молярна маса; СР, СV – теплоємність газу при сталому тиску і об’ємі.
- молярна маса; СР, СV – теплоємність газу при сталому тиску і об’ємі.
Знайдемо відношення А до DQ і DU до DQ:
 , (85)
, (85)
 . (86)
. (86)
У випадку двохатомного газу число ступенів вільності молекули газу і =5, звідси:
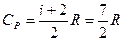 , (87)
, (87)
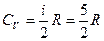 . (88)
. (88)
З урахуванням співвідношень (87) та (88) вирази (85), (86) набудуть вигляду
 , (89)
, (89)
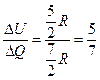 . (90)
. (90)
Із рівнянь (89) і (90) отримаємо
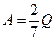 ,
, 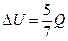 . (91)
. (91)
Підставивши у (91) значення фізичних величин, отримаємо:
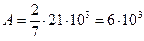 Дж,
Дж,
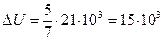 Дж.
Дж.
Відповідь: А = 6×103 Дж; D Q = 15×103 Дж.
Приклад 16 Яку роботу  треба виконати при видуванні мильної бульбашки, щоб збільшити її об’єм від
треба виконати при видуванні мильної бульбашки, щоб збільшити її об’єм від 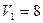 см
см 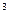 до
до  16 см
16 см 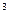 (рис.15)? Вважати процес ізотермічним.
(рис.15)? Вважати процес ізотермічним.
 |
Рисунок 15 - Зміна об’єму мильної бульбашки в процесі її роздування
Розв’язання. Робота, яка здійснюється при видуванні мильної бульбашки, йде на приріст енергії її поверхні:
А=Е2-Е1 , (92)
де Е1, Е2 – енергія у кінцевому та початковому станах бульбашки.
У мильної бульбашки є дві поверхні – зовнішня та внутрішня, площі яких майже однакові через малу товщину мильної плівки, тому вільна енергія поверхні (внутрішньої та зовнішньої разом) мильної бульбашки дорівнює
Е1=2sS1, (93)
E2=2sS2, (94)
де s - коефіцієнт поверхневого натягу; S1, S2 – площа поверхні бульбашки в початковий момент і в кінці процесу.
Врахуємо, що площа поверхні сфери дорівнює
S1=4pr12, (95)
S2=4pr22, (96)
де r1 та r2 - радіуси бульбашок на початку та в кінці процесу.
Відповідні радіуси бульбашок знайдемо, знаючи, що об’єм
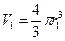 , Þ
, Þ 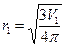 , (97)
, (97)
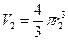 ,Þ
,Þ  . (98)
. (98)
З урахуванням співвідношень (92)-(98) отримаємо
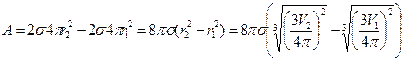 . (99)
. (99)
Підставивши числові значення фізичних величин в співвідношення (95), отримаємо
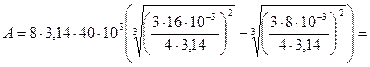 =
= 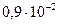 Дж.
Дж.
Перевіримо розмірність фізичної величини.
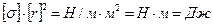 .
.
Відповідь: А = 0,9×10-2 Дж.
Приклад 17 Три точкові заряди 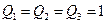 нКл розташовані у вершинах рівностороннього трикутника (рис.16). Який заряд
нКл розташовані у вершинах рівностороннього трикутника (рис.16). Який заряд  потрібно помістити в центрі трикутника, щоб система зарядів знаходилася в рівновазі?
потрібно помістити в центрі трикутника, щоб система зарядів знаходилася в рівновазі?
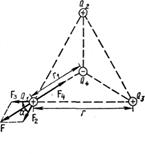
Рисунок 16 – Умова рівноваги системи зарядів
Розв’язання. Всі три заряди, розташовані у вершинах трикутника, знаходяться в однакових умовах. Тому достатньо розглянути умову рівноваги будь-якого з трьох зарядів, наприклад 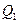 . Заряд
. Заряд 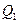 буде знаходитися в рівновазі, якщо векторна сума сил, що діють на нього, дорівнює нулю (рис.16):
буде знаходитися в рівновазі, якщо векторна сума сил, що діють на нього, дорівнює нулю (рис.16):
 (100)
(100)
де  - сили, з якими відповідно діють на заряд
- сили, з якими відповідно діють на заряд 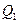 заряди
заряди 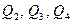 ;
;  - рівнодійна сил
- рівнодійна сил 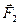 і
і 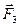 .
.
Оскільки сили  і
і 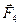 направлені за однією прямою у протилежні сторони, векторну рівність (100) можна замінити скалярною: F -
направлені за однією прямою у протилежні сторони, векторну рівність (100) можна замінити скалярною: F - 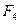 = 0, звідки
= 0, звідки 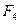 = F. Виразимо в останньому співвідношенні F через
= F. Виразимо в останньому співвідношенні F через 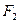 і
і 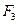 . Враховуючи, що
. Враховуючи, що 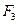 =
= 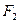 , отримаємо
, отримаємо
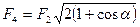 .
.






