1 Рівняння Ван-дер-Ваальса для одного моля газу
,
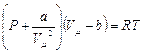для довільної кількості речовини v газу
,
де a і b – сталі Ван-дер-Ваальса (розраховані на один моль газу); V — об’єм, що займає газ; Vm - молярний об’єм; Р - тиск газу на стінки посудини.
, або 
- внутрішній тиск, зумовлений силами взаємодії молекул.
2 Зв’язок критичних параметрів - об’єму, тиску і температури газу зі сталими a і b Ван-дер-Ваальса
, 
, 
.
3 Внутрішня енергія реального газу
,
де CV – молярна теплоємність газу при сталому об’ємі.
4 Коефіцієнт поверхневого натягу
,
де F – сила поверхневого натягу, що діє на контур l, який обмежує поверхню рідини, або
,
де ΔE – зміна вільної енергії поверхневої плівки рідини при зміні площі ΔS поверхні цієї плівки.
5 Формула Лапласа в загальному випадку
,
де Р – тиск, який створює вигнута поверхня рідини; σ – коефіцієнт поверхневого натягу; R1 і R2 - радіуси кривини двох взаємно перпендикулярних перерізів поверхні рідини.
Якщо поверхня сферична,
.
6 Висота, на яку піднімається рідина в капілярній трубці,
,
де q – крайовий кут; R – радіус каналу трубки; ρ – густина рідини; g – прискорення вільного падіння.
7 Висота, на яку піднімається рідина між двома близькими паралельними площинами,
,
Де d – відстань між площинами.
Електричне поле у вакуумі
1 Закон Кулона
,
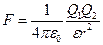де F – сила взаємодії двох точкових зарядів Q1 та Q2; r - відстань між зарядами; ε - діелектрична проникність середовища; ε0 - електрична стала,
.
2 Закон збереження заряду
,
де 
– алгебраїчна сума зарядів, що входять до ізольованої системи; n - кількість зарядів.
3 Напруженість електричного поля
,
де 
– сила, що діє на точковий заряд Q, який поміщений в дану точку поля.
Сила, що діє на точковий заряд Q, розміщений в електричному полі, дорівнює
.
4 Потік вектора напруженості 
електричного поля:
а) через довільну поверхню S, яка поміщена в неоднорідне поле,
, або 
,
де α – кут між вектором напруженості і нормаллю 
до елемента поверхні; dS – площа елемента поверхні; En – проекція вектора напруженості на нормаль;
б) через плоску поверхню, яка поміщена в однорідне електричне поле,
.
Потік вектора напруженості через замкнену поверхню S
,
де інтегрування ведеться по всій поверхні.
5 Теорема Гауса в інтегральній формі. Потік вектора напруженості електричного поля через будь-яку замкнену поверхню дорівнює алгебраїчній сумі зарядів, що обмежуються цією поверхнею, поділеній на 
.
,
де - алгебраїчна сума зарядів, що містяться в цій замкненій поверхні; n – кількість зарядів.
Теорема Гауса у диференціальній формі
,
де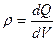 
- об’ємна густина заряду, у даній точці простору; Q, V – відповідно заряд та об’єм цієї області.
6 Напруженість електричного поля точкового заряду Q на відстані r від заряду,
.
7 Напруженість електричного поля металевої сфери радіуса R, що має заряд Q, на відстані r від центра сфери:
- всередині сфери (r < R) …………… E = 0,
- на поверхні сфери (r = R) ……. 
,
- поза сферою (r > R) …………… .
8 Принцип суперпозиції (накладання) електричних полів: напруженість результуючого поля, створеного двома (і більше) точковими зарядами, дорівнює векторній (геометричній) сумі напруженостей полів, створених у даній точці окремими зарядами:
.
У випадку двох електричних полів з напруженостями 
і 
абсолютне значення вектора напруженості дорівнює
,
де α – кут між векторами 1 і 2.
9 Напруженість поля, створеного нескінченно довгою рівномірно зарядженою ниткою (або циліндром) на відстані r від її осі,
,
де τ – лінійна густина заряду.
У випадку циліндра радіусом 
формула справедлива при 
. При 
- 
.
Лінійна густина заряду - це величина, яка дорівнює відношенню заряду, розподіленому вздовж нитки, до довжини нитки (циліндра):
.
10 Напруженість поля, яке створює нескінченна рівномірно заряджена площина,
,
де σ – поверхнева густина заряду.
Поверхнева густина заряду - це величина, яка дорівнює відношенню заряду, розподіленого по поверхні, до площі цієї поверхні:
.
11 Напруженість поля, що створюється двома паралельними нескінченними рівномірно і різнойменно зарядженими площинами, з однаковою за абсолютним значенням поверхневою густиною σ заряду (поле плоского конденсатора)
.
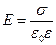Наведена формула справедлива для обчислення напруженості поля між пластинами плоского конденсатора (в середній його частині) лише в тому випадку, якщо відстань між пластинами значно менша лінійних розмірів пластин конденсатора.
12 Циркуляція вектора напруженості електричного поля - це величина, яка чисельно дорівнює роботі по переміщенню одиничного точкового позитивного заряду по замкненому контуру. Циркуляція визначається інтегралом по замкнутому контуру 
, де El – проекція вектора напруженості в даній точці контуру на напрямок дотичної до контуру в тій самій точці.
У випадку електростатичного поля циркуляція вектора напруженості дорівнює нулю:
.
13 Потенціал електричного поля - це величина, що дорівнює відношенню потенціальної енергії заряду, який поміщений у дану точку поля, до величини цього заряду
,
або потенціал електричного поля - це величина, яка дорівнює відношенню роботи сил поля по переміщенню точкового позитивного заряду із даної точки поля у нескінченність до величини цього заряду:
.
14 Потенціал електричного поля у нескінченності умовно взятий за нуль. При переміщенні заряду в електричному полі робота Aз.с зовнішніх сил дорівнює за абсолютним значенням роботі Ас.п сил поля і протилежна їй за знаком:
.
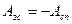15 Потенціал електричного поля, створюваного точковим зарядом Q на відстані r від заряду,
.
16 Потенціал електричного поля, створюваного металевою сферою радіуса R, яка несе заряд Q, на відстані r від центру сфери:
- в середині сфери (r < R) 
,
- на поверхні сфери (r = R) ,
- поза сферою (r > R) 
.
17 Потенціал електричного поля, створеного системою n точкових зарядів, в даній точці за принципом суперпозиції електричних полів дорівнює алгебраїчній сумі потенціалів φ1, φ2..., φn, створених окремими точковими зарядами Q 1, Q 2,..., Qn:
.
18 Енергія E взаємодії системи точкових зарядів Q 1, Q 2,..., Qn визначається роботою, яку ця система зарядів може здійснити за умови віддалення їх один відносно одного у нескінченність, і визначається формулою
,
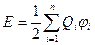де φi – потенціал поля, яке створюється усіма n-1 зарядами (за винятком i -го) у точці, де розміщений заряд Qi.
19 Потенціал пов’язаний із напруженістю електричного поля співвідношенням
.
Для електричного поля із сферичною симетрією цей зв’язок має вигляд
,
або, в скалярній формі,
,
а у випадку однорідного поля, тобто поля, напруженість якого у кожній точці однакова як за абсолютним значенням, так і за напрямком,
,
де φ1 і φ2 – потенціали точок двох еквіпотенціальних поверхонь; d – відстань між цими поверхнями вздовж електричної силової лінії.
20 Робота, що здійснюється електричним полем при переміщенні точкового заряду Q із однієї точки поля з потенціалом φ1, в іншу з потенціалом φ2,
, або 
,
де El – проекція вектора напруженості на напрямок переміщення; dl – переміщення.
Для однорідного поля остання формула набуває вигляду
,
де 
– переміщення; α – кут між напрямами вектора і переміщення .
12 Електричне поле у діелектриках
1 Диполь – це система двох точкових, рівних за модулем і протилежних за знаком зарядів, які розміщені на деякій відстані один від одного.
Електричний момент 
диполя - це вектор, напрямлений від негативного заряду до позитивного, який дорівнює добутку заряду | Q | на вектор , що проведений від негативного заряду до позитивного і має назву “плече диполя”, тобто
.
Диполь має назву точкового, якщо плече l диполя значно менше відстані r від центра диполя до точки, у якій визначається дія диполя (l << r).
2 Напруженість поля точкового диполя
,
де – електричний момент диполя; r – абсолютне значення радіуса-вектора, який проведений від центра диполя до точки, в якій визначається напруженість поля; α – кут між радіусом-вектором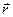 
та плечем диполя.
Напруженість поля точкового диполя у точці, яка лежить на осі диполя (α = 0),
,
а в точці, яка лежить на перпендикулярі до плеча диполя, що проведений із його середини (α = π/2),
.
3 Потенціал поля точкового диполя
.
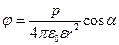Потенціал поля точкового диполя в точці, яка лежить на осі диполя (α = 0),
,
а в точці, яка лежить на перпендикулярі до плеча диполя, що проведений із його середини (α = π/2),
.
Напруженість і потенціал неточкового диполя визначаються так само, як для системи зарядів.
4 Механічний момент, який діє на диполь з електричним моментом , поміщений в однорідне електричне поле з напруженістю ,
, або 
,
де α – кут між напрямками векторів та .
У неоднорідному електричному полі, окрім механічного моменту (пари сил), на диполь діє ще деяка сила. У випадку поля, яке має симетрію відносно осі x, ця сила визначається співвідношенням
,
де 
- часткова похідна напруженості поля, яка характеризує ступінь неоднорідності поля у напрямку осі x.
При α >π/2 сила Fx позитивна. Це означає, що під її дією диполь втягується в область сильного поля.
5 Поляризованість діелектрика
,
де V – об’єм діелектрика; pi - дипольний момент i –ї молекули.
Зв’язок між поляризованістю діелектрика і напруженістю електростатичного поля
,
де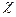 
- діелектрична сприйнятливість речовини.
Зв’язок діелектричної проникності 
з діелектричною сприйнятливістю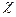
.
Зв’язок між напруженістю Е поля в діелектрику і напруженістю Е0 зовнішнього поля
.
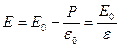Електричне зміщення 
пов’язане з напруженістю електричного поля співвідношенням
.
Це співвідношення справедливе лише для ізотропних діелектриків.
6 Потік вектора електричного зміщення визначається аналогічно потоку вектора напруженості електричного поля:
- у випадку однорідного поля
;
- у випадку неоднорідного поля і довільної поверхні
,
де Dn – проекція вектора на напрямок нормалі до елемента поверхні, площа якої дорівнює d S.
7 Теорема Гауса. Потік вектора електричного зміщення через будь-яку замкнену поверхню дорівнює алгебраїчній сумі сторонніх зарядів, які містяться всередині цієї поверхні:
,
де n – кількість сторонніх зарядів (як додатних, так і від’ємних), що знаходяться всередині замкненої поверхні.
13 Провідники в електричному полі
1 Електроємність ізольованого провідника або конденсатора
,
де dQ – заряд, переданий провіднику (конденсатору); dφ – зміна потенціалу, яка викликана цим зарядом.
2 Електроємність ізольованої провідникової сфери радіусом R, яка поміщена у нескінченне середовище з діелектричною проникністю ε,
.
Якщо сфера порожня і заповнена діелектриком, то електроємність її від цього не змінюється.
3 Електроємність плоского конденсатора
,
де S – площа кожної з пластин; d – відстань між ними;
ε – діелектрична проникність діелектрика, який заповнює простір між пластинами.
Електроємність плоского конденсатора, який заповнений n шарами діелектрика товщиною di кожний, діелектричні проникності яких εi (шаруватий конденсатор),
.
4 Електроємність сферичного конденсатора (дві концентричні сфери радіусами R1 і R2, простір між якими заповнено діелектриком з діелектричною проникністю ε)
.
5 Електроємність циліндричного конденсатора (два коаксіальних циліндри довжиною l і радіусами R1 і R2, простір між якими заповнено діелектриком з діелектричною проникністю ε)
.
6 Електроємність послідовно з’єднаних конденсаторів:
- у загальному випадку 
,
де n – кількість конденсаторів;
- у випадку двох конденсаторів 
;
- у випадку n однакових конденсаторів з електроємністю C1 кожний 
.
7 Електроємність паралельно з’єднаних конденсаторів:
- в загальному випадку 
,
де n – кількість конденсаторів;
- у випадку двох конденсаторів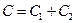 
;
- у випадку n однакових конденсаторів з електроємністю C1 кожний 
.
14 Енергія електричного поля
1 Енергія зарядженого провідника пов’язана із зарядом Q, потенціалом φ та електроємністю C провідника співвідношеннями:
.
2 Енергія зарядженого конденсатора
,
де C – електроємність конденсатора; U – різниця потенціалів на його пластинах.
3 Об’ємна густина енергії (енергія електричного поля, що припадає на одиницю об’єму)
,
де – напруженість електричного поля в середовищі з діелектричною проникністю ε; – електричне зміщення.
16 Електричний струм
1 Сила постійного струму
,
де Q – заряд, що пройшов через поперечний переріз провідника за час t.
2 Густина електричного струму - це векторна величина, яка дорівнює відношенню сили струму до площі S поперечного перерізу провідника
,
де 
– одиничний вектор, який за напрямком збігається з напрямком руху позитивних носіїв заряду.
3 Опір однорідного провідника
,
де ρ – питомий опір речовини провідника; l – його довжина.
4 Провідність W провідника і питома провідність s речовини
, 
.
5 Залежність питомого опору від температури
,
де ρ і ρ0 – питомі опори відповідно при t і 00 С; t – температура (за шкалою Цельсія); α – температурний коефіцієнт опору.
6 Опір з’єднаних провідників:
- послідовно 
;
- паралельно 
,
де Ri – опір i -го провідника; n – кількість провідників.
7 Закон Ома в інтегральній формі:
- для неоднорідної ділянки кола 
;
- для однорідної ділянки кола (
= 0) 
;
- для замкненого кола (φ1 = φ2) 
,
де (φ1 - φ2) – різниця потенціалів на кінцях ділянки кола; – ЕРС джерел струму, що входять у цю ділянку; U – напруга на ділянці кола; R – опір кола (дільниці кола); – EPC усіх джерел струму у колі.
8 Правила Кірхгофа
Перше правило: алгебраїчна сума сил струмів, що сходяться у вузлі, дорівнює нулю, тобто
,
де n – кількість струмів, що сходяться у вузлі.
Вузол – це точка кола, куди сходяться більше двох провідників.
Друге правило: у замкненому контурі алгебраїчна сума напруг на всіх ділянках контуру дорівнює алгебраїчній сумі електрорушійних сил, тобто
,
де Ii – сила струму на i -й ділянці; Ri – активний опір на i -й ділянці; 
– EPC джерел струму на i -й ділянці; n – кількість ділянок, що містять активний опір; k – кількість ділянок, що містять джерела струму.
9 Робота, яка здійснюється електростатичним полем і сторонніми силами на ділянці кола постійного струму за час t,
.
10 Потужність струму
.
11 Закон Джоуля-Ленца
,
де Q –кількість теплоти, що виділяється на ділянці кола за час t.
Закон Джоуля-Ленца має місце за умови, що ділянка кола нерухома і в ній не здійснюються хімічні перетворення.
12 Густина струму 
, середня швидкість < 
> впорядкованого руху носіїв заряду та їх концентрація n пов’язані співвідношенням
,
де e – елементарний заряд.
13 Закон Ома у диференціальній формі
,
де s – питома провідність провідника; – напруженість електричного поля.
14 Закон Джоуля-Ленца у диференціальній формі
,
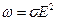де ω – об’ємна густина теплової потужності.
15 Формула Річардсона-Дешмана
,
де 
- густина струму насичення термоелектронної емісії; С – стала, теоретично однакова для всіх металів: А - робота виходу електронів з металу.
15 Закони електролізу Фарадея.
Перший закон
,
де m – маса речовини, що виділилася на електроді під час проходження через електроліт електричного заряду Q; k – електрохімічний еквівалент речовини.
Другий закон
,
де F – стала Фарадея (F = 96,5 кКл/моль); m – молярна маса іонів даної речовини; Z – валентність іонів.
Об’єднаний закон
,
де I – сила струму, що проходить через електроліт; t – час, протягом якого проходить струм.
16 Рухливість іонів
,
де <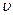 
> - середня швидкість впорядкованого руху іонів;
E – напруженість електричного поля.
17 Закон Ома у диференціальній формі для електролітів і газів при самостійному розряді в області, яка далека від насичення,
,
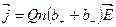де Q – заряд іона; n – концентрація іонів; b+ і b- - рухливість відповідно позитивних і негативних іонів.
18 Густина струму насичення
,
де n0 – кількість пар іонів, що створює іонізатор у одиниці об’єму за одиницю часу; d – відстань між електродами (
, де N – кількість пар іонів, що створює іонізатор за час t у просторі між електродами; V – об’єм цього простору).
