Перша частина
Зведення основних формул
1 Кінематика
1 Положення матеріальної точки у просторі задається радіусом-вектором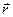 
:
,
де 
– орти; x, y, z – координати точки.
Кінематичні рівняння руху в координатній формі мають такий вигляд:
,
де t – час.
2 Середня швидкість
,
де 
- переміщення матеріальної точки за інтервал часу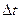 
.
Середня швидкість на шляху ΔS:
,
де ΔS – шлях, який пройшла точка за інтервал часу .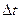
Миттєва швидкість
,
де 
- проекції вектора швидкості 
на осі координат.
Абсолютне значення швидкості
Прискорення
,
де 
- проекції вектора прискорення 
на осі координат.
Абсолютне значення прискорення
При криволінійному русі прискорення є сумою нормальної і тангенціальної складових
,
де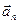 
і 
– відповідно нормальне і тангенціальне прискорення. Модулі цих величин дорівнюють 
, де R – радіус кривини у даній точці траєкторії Тоді можна записати
,
Кінематичне рівняння рівномірного руху матеріальної точки вздовж осі x має вигляд
,
де x0 – початкова координата.
При рівномірному русі 
.
5 Кінематичне рівняння рівнозмінного руху (a = const) вздовж осі x
,
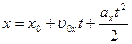де 
– початкова швидкість.
Швидкість точки при рівнозмінному русі
.
6 Положення в просторі твердого тіла при обертанні визначається кутом повороту радіуса-вектора 
. Кінематичне рівняння обертального руху має такий вигляд:
,
де φ – кут повороту (або кутове переміщення).
7 Середня кутова швидкість
,
де Δφ – зміна кута повороту за час Δt.
Миттєва кутова швидкість
.
Кутове прискорення
.
9 Кінематичне рівняння рівномірного обертання
.
При рівномірному обертанні 
.
Частота обертання
, або 
,
де N – число обертів, що здійснюється за час t; T – період обертання (час одного повного оберту).
10 Кінематичне рівняння рівнозмінного обертання (ε = =const)
.
Кутова швидкість тіла при рівнозмінному русі
.
11 Зв’язок між лінійними та кутовими величинами, що характеризують обертання матеріальної точки, задається такими співвідношеннями:
довжина шляху, який пройшла точка
по дузі кола радіусом R – 
;
лінійна швидкість точки – 
;
прискорення точки:
– тангенціальне – 
;
– нормальне – 
.
2 Динаміка поступального руху
1 Рівняння руху матеріальної точки (другий закон Ньютона) у векторній формі має вигляд
або у випадку, коли 
, 
,
де 
- геометрична сума сил, що діють на матеріальну точку; m –маса; – прискорення; 
– імпульс; N – кількість сил, що діють на точку;
у координатній (скалярній) формі
або
, 
, 
,
де під знаком суми знаходяться проекції сил Fi на відповідні осі координат.
2 Сила пружності
,
де k – коефіцієнт пружності; x – абсолютна деформація.
3 Сила гравітаційної взаємодії двох точкових тіл
,
де G - гравітаційна стала; m1 і m2 –маси тіл, що взаємодіють; r – відстань між тілами.
4 Сила тертя ковзання
,
де 
– коефіцієнт тертя; N - сила нормального тиску.
5 Координати центра мас системи матеріальних точок
, 
, 
,
де mi – маса i -ї матеріальної точки; xi, yi, zi – її координати.
3 Закони збереження імпульсу і енергії
1 Імпульс матеріальної точки
.
Закон збереження імпульсу для ізольованої системи
, або 
,
де N – кількість матеріальних точок (тіл) системи.
2 Робота, яка здійснюється сталою силою:
, або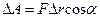 
,
де α – кут між напрямками векторів сили 
та переміщення .
3 Робота, яка здійснюється змінною силою:
,
де інтегрування ведеться вздовж траєкторії L.
4 Середня потужність за інтервал часу Δt
.
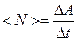5 Миттєва потужність
, або 
.
6 Кінетична енергія матеріальної точки (тіла, що рухається поступально)
, або 
.
7 Потенціальна енергія тіла і сила, що діє на тіло в даній точці поля, пов’язані співвідношенням
, або 
,
де 
– орти. Якщо поле сил має сферичну симетрію, одержимо
.
8 Потенціальна енергія пружно-деформованого тіла
.
9 Потенціальна енергія гравітаційної взаємодії двох матеріальних точок (тіл) масами m1 і m2, що знаходяться на відстані r:
.
10 Потенціальна енергія тіла, що міститься в однорідному полі сили тяжіння:
,
де h (h<<R) – висота тіла над нульовим рівнем; R - радіус Землі.
11 Консервативними називаються сили, робота яких по замкнутому контуру дорівнює нулю:
.
В ізольованій системі, в якій діють тільки консервативні сили, виконується закон збереження енергії
.
