Эквиваленция высказываний. Тавтологии

Определение. Составное высказывание, образованное из двух элементарных словами «если и только если» и обозначаемое А Û В, называют эквиваленцией. Эквиваленция двух высказываний А и В истинна тогда и только тогда, когда оба высказывания А и В истинны или оба ложны.

Таблица истинности эквиваленции имеет вид (табл. 14).

Таблица 14

A	B	А Û В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Например: высказывание «Число 200 делится на 10 тогда и только тогда, когда 200 оканчивается 0» истинно. Употребляя Û, можем записать А Û В.

Определение. Составные высказывания, истинные при любых предположениях об истинности входящих в них элементарных высказываний, называют тавтологиями.

Примеры тавтологий: A Ú B Û B Ú A; А Ù В Û В Ù А;

((А Þ В) Ù А) Þ В. Составим таблицу истинности для последней формулы (табл. 15).

Таблица 15

А	В	А Þ В	(А Þ В) Ù А	((А Þ В) Ù А) Þ В
И	И	И	И	И
Л	И	И	Л	И
И	Л	Л	Л	И
Л	Л	И	Л	И

 

Последняя тавтология означает, что если истинна импликация А Þ В и истинно условие А, то истинно и следствие В.

Одноместные предикаты

Определение. Предложение с переменной х, где х Î Х, называют одноместным предикатом или одноместной высказывательной формой, если при подстановке любого значения х Î Х получается высказывание. Одноместные предикаты обозначают символами А (х), х Î Х; В (х), х Î Х и т.д.

X – это множество значений, которые может принимать переменная х, его называют областью определения предиката. Каждый предикат А (х), х Î Х определяет подмножество Т Í Х, состоящее из элементов, при подстановке которых в А (х) вместо х получается истинное высказывание. Это подмножество называется множеством истинности предиката. Например, предложение «х – простое число», заданное на множестве N – натуральных чисел, является высказывательной формой. При подстановке вместо х числа 3 получается истинное высказывание: «3 – простое число». При подстановке вместо х числа 10 – ложное высказывание: «10 – простое число». Высказывательная форма порождает множество высказываний одной и той же формы. Множеством истинности заданного предиката является множество всех простых чисел.

Одноместный предикат является ни чем иным, как характеристическим свойством, позволяющим выделить из области определения этого предиката подмножество истинности Т.

Пусть предикат А (х): «Город х – столица Башкортостана» задан на множестве X – городов Башкортостана. Ясно, что А (х) определяет характеристическое свойство: быть столицей Башкортостана.

Область истинности Т = { х | А (х)} = {Уфа}. Предикат разбивает область определения на два подмножества, на одном из которых он принимает истинные значения, а на другом – ложные.

Замечание. Переменная в предикате может содержаться неявно. Например, предложение «диагонали параллелограмма взаимно перпендикулярны» является предикатом, хотя в него явно не входит переменная, а лишь подразумевается. Если параллелограмм, о котором говорится в предикате, является ромбом, то получим истинное высказывание. Ясно, что множеством истинности (Т) этого предиката является множество ромбов.

Предикаты, заданные на конечных множествах, можно задавать таблицами, в первой строке которых указывается элемент множества, а во второй – истинность или ложность высказывания, получаемого из предиката, если заменить переменную этим элементом. Например, предикат x + 24 > 40, заданный на множестве X = {14, 15, 16, 17, 18, 19}, можно задать таблицей (табл. 16).

Таблица 16

х
x + 24 > 40	Л	Л	Л	И	И	И

 

Может случиться, что два предиката А (х) и В (х), заданные на одном и том же множестве X имеют одинаковые множества истинности. Такие предикаты называются эквивалентными. Их обозначают так: А (х) ~ В (х).

П р и м е р ы эквивалентных предикатов:

1) А (х): х + 15 = 25, x Î R и В (х): 5 х = 50, x Î R.

2) А (х): «натуральное число х делится на 5» и В (х): «натуральное число х оканчивается 0 или 5».

3) А (х): 2 х + 2 > 10, х Î R и В (х): х + 1 > 5, x Î R.

Многоместные предикаты

Пусть некоторое предложение В (х, у) содержит две переменные, причем переменная х принимает значения из X, а переменная у из Y (эти множества могут и совпадать). Все пары (х, у), где х Î Х и у Î Y, образуют, как уже знаем, декартово произведение X ´ Y. Пусть для любой пары (а, в) из X ´ Y при замене в предложении В (х, у) переменной x ее значением а, переменной у ее значением в, получается высказывание В (а, в), тогда такое предложение В (х, у) называется двухместным предикатом, заданным на множестве X ´ Y.

Совокупность Т пар (а, в), при подстановке которых в двухместный предикат В (х, у) получается истинное высказывание, называется множеством истинности этого предиката. Это множество является подмножеством декартова произведения X ´ Y.

П р и м е р ы двухместных предикатов.

1) «Треугольник х равен треугольнику у». Здесь X, Y – множество треугольников, Т – множество пар равных треугольников.

2) х < у, x Î Z, y Î Z. T = {(х, y)Î Z ² | х < у }.

3) х ² + y ² = 1, x Î R, y Î R. Т = {(х, y) Î R ² | х ² + у ² = 1}.

Как в случае одноместных предикатов двухместные предикаты называют эквивалентными, если области определения и множества истинности этих предикатов совпадают.

Например, неравенства х + y > 5 и 2 х + 2 y > 10 эквивалентные предикаты на множестве R. Им удовлетворяет одно и тоже множество пар.

Аналогично определяются трехместные, четырехместные и т.д.,
n -местные предикаты.

Кванторы

Рассмотрим операции, преобразующие предикаты в высказывания. Одной из таких операций является подстановка вместо переменных их значений. Например, подставим вместо переменных х, у в двухместном предикате А (х, у): «х делится на у» пару чисел (6, 2) получим высказывание: «6 делится на 2» – «И». Подставим пару чисел (5, 2), получим высказывание «5 делится на 2» – «Л».

Другой операцией, преобразующей предикат в высказывание, является операция связывания кванторами.

1. Выражение «для всех х» (для всякого х, для каждого х, для любого х) называют квантором общности и обозначают символом (" х).

2. Выражение «существует х» (найдется х, существует хотя бы один х) называют квантором существования и обозначают символом ($ х).

Различают эти два основных вида квантора. Квантор существования имеет еще одну разновидность, а именно: выражение «существует точно один х» называется квантором существования и единственности и обозначается символом ($! х).

Высказывание (" x Î X) В (х) читают: «для любого х из X выполняется (справедливо) В (х)».

Высказывание ($ х Î Х) В (х) читают: «существует такое х из X, что выполняется (справедливо) В (х)».

Высказывание ($! х Î Х) В (х) читают: «существует точно одно значение х из Х, что справедливо В (х)».

Приведем п р и м е р употребления кванторов.

Пусть задан предикат х < 5, x Î R.

Используя кванторы, запишем следующие высказывания:

(" x Î R) [ х < 5] (для всякого x Î R выполняется неравенство х < 5) – это ложное высказывание. ($ х Î R) [ x < 5] (существует х Î R, такое, что х < 5) – это истинное высказывание. ($! х Î R) [ x < 5] (существует точно одно значение х Î R, такое, что x < 5) – это ложное высказывание.

Все сказанное выше о связывании кванторами в одноместных предикатах остается справедливым и для многоместных предикатов, только для получения из них высказываний надо связать квантором каждую переменную. Например, если дан предикат «число х меньше числа y», то из него можно получить, например, такие высказывания (" x Î R) (" y Î R) [ x < y ] или ($ х Î R) ($ y Î R) [ x < y ].

Замечание. Если рядом стоят несколько одноименных кванторов по переменным с одной областью определения, то условились писать знак квантора только один раз, перечислив за ним все эти переменные.

В силу этого замечания, приведенный выше пример, запишется так:

(" х, y Î R)[ x < y ] или ($ х, y Î R)[ x < y ].

Возникает вопрос, как установить значение истинности высказывания с кванторами.

Истинность высказывания с квантором общности устанавливается путем доказательства. Чтобы установить ложность такого высказывания достаточно привести контрпример. Дело в том, что квантор общности можно рассматривать как обобщение конъюнкции, а квантор существования как обобщение дизъюнкции. По этой же причине отрицание высказывания с квантором общности равносильно высказыванию с квантором существования, после которого стоит отрицание предложения, т.е.

Û .

Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Ложность такого высказывания устанавливается путем доказательства. Отрицание высказывания с квантором существования равносильно высказыванию с квантором общности, после которого стоит отрицание предложения, т.е. Û .

Операции над предикатами

Предикаты, так же как и высказывания, бывают элементарными и составными. Составные предикаты образуются из элементарных при помощи логических операций: отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции. Смысл этих операций тот же, что и в логике высказываний.

Установим правила, которые позволяют найти множество истинности составного предиката, если известны множества истинности составляющих его элементарных предикатов.

Пусть на множестве Х задан предикат А (х). Его отрицанием называют предикат , определённый на том же множестве Х, причём предикат – «И» при тех значениях х из Х, при которых А (х) – «Л», и наоборот.

П р и м е р. На множестве Х = {10, 15, 20, 21, 19, 17} рассмотрим предикат А (х): «х кратно 3». Тогда : «х не кратно 3». Легко видеть, что множеством истинности предиката А (х) является Т = {15, 21}, а для множеством истинности является = {10, 20, 19, 17}, т.е. дополнение к множеству Т.

Вообще, если Т – множество истинности предиката А (х), х Î Х, то множеством истинности предиката , х Î Х является (дополнение к Т в множестве Х). Запишем эти множества символически:

Т = { х Î Х | А (х)} .

Изобразим множество истинности предиката на диаграмме Эйлера-Венна заштрихованной областью (рис. 2).

 

Пусть теперь на множестве Х заданы два предиката А (х) и В (х). Образуем их конъюнкцию, т.е. А (х) Ù В (х). Полученный предикат истинный при тех значениях х Î Х, при которых «И» оба предиката А (х) и В (х).

П р и м е р. На множестве Х = {10, 15, 16, 20, 35} заданы предикаты А (х): «число х – чётное» и В (х): «х кратно 5». А (х) Ù В (х) обращается в истинное высказывание, если х Î {10, 20}. Обозначим Т ₁ = {10, 16, 20} – множество истинности предиката А (х), Т ₂ = {10, 15, 20, 35} – множество истинности предиката В (х), тогда ={10, 20}.

Вообще, если Т₁ – множество истинности предиката А (х), х Î Х, а Т ₂ –множество истинности предиката В (х), х Î Х, то множество истинности Т предиката А (х) Ù В (х), х Î Х есть пересечение множеств Т ₁ и Т ₂. Запишем это множество символически:

}.

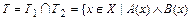Изобразим множество истинности предиката на диаграмме Эйлера-Венна заштрихованной областью (рис. 3).

 

 

Рис. 3

Предикат А (х) Ú В (х), называют дизъюнкцией предикатов А (х),
х Î Х и В (х), х Î Х. Он истинный при тех значениях х из Х, при которых истинный хотя бы один из предикатов А (х) и В (х).

П р и м е р. Пусть предикат А (х): «х – студент I курса»; а предикат В (х): «х – спортсмен», заданные на X – множестве студентов некоторого института. Тогда A (x) Ú B (x) предикат: «студент х спортсмен или первокурсник".

Вообще, если Т ₁ – множество истинности предиката А (х), а Т ₂ – множество истинности предиката В (х), то множеством истинности предиката A (x) Ú B (x), х Î Х является множество . Запишем это множество символически:

Х

Изобразим множество истинности предиката на диаграмме Эйлера-Венна заштрихованной областью (рис. 4).

 

 

Составим теперь импликацию двух предикатов А (х) Þ В (х), где предикаты А (х) и В (х) заданы на некотором множестве X.

Предикат А (х) Þ В (х) превращается в ложное высказывание при подстановке вместо х таких значений а, при которых А (а) – «И», В (а) – «Л». Если T ₁ – множество истинности предиката А (х), T ₂ – множество истинности предиката В (х), то импликация А (х) Þ В (х) ложна на множестве , а на дополнении к этому множеству предикат
А (х) Þ В (х) истинный. Найдем это дополнение. По закону де Моргана: .

Значит, множеством истинности предиката А (х) Þ В (х) является объединение множества T ₂ (истинности предиката В (х)) и дополнения к множеству T ₁ (истинности предиката А (х)). Запишем это множество символически

Изобразим множество истинности предиката А (х) Þ В (х) на диаграмме Эйлера-Венна заштрихованной областью (рис. 5)

 

Рис. 5

Часто встречаются такие предикаты, что для всех значений х Î Х из истинности одного следует истинность другого. Например, из предиката А (х): «х делится на 4», следует В (х): «х делится на 2». Оба предиката определены на множестве натуральных чисел.

Рис. 6

Из истинности некоторого предиката А (х) следует истинность предиката В (х) в том и только в том случае, когда пусто (на котором предикат А (х) Þ В (х) ложен). Множества T ₁ и имеют пустое пересечение, если T ₁ Ì T ₂ (как изображено на рис. 6). В том случае, когда импликация А (х) Þ
Þ В (х), х Î Х истинна при всех значениях x, говорят, что В (х) логически следует из А (х) и для их множеств истинности выполняется , где Т₁ – множество истинности А (х),
Т ₂ – множество истинности В (х). Тогда предикат В (х) называют необходимым условием для А (х), предикат А (х) достаточным условием для В (х).

Если предикат А (х) Û В (х) задан на множестве X, то каждый из предикатов А (х) и В (х) называют необходимым и достаточным условием для другого. Например, для того, чтобы натуральное число х делилось на 10, необходимо и достаточно, чтобы последняя цифра в десятичной записи этого числа была равна 0. Запишем множество истинности Т предиката

А (х) Û В (х) символически:

.

Изобразим множество истинности предиката А (х) Û В (х) на диаграмме Эйлера-Венна заштрихованной областью (рис. 7).

Строение теоремы

Каждая математическая теория представляет собой множество предложений. Среди них некоторые предложения принимаются за исходные (аксиомы) так, чтобы все остальные предложения этого множества (теоремы) логически следовали из них. Всякое математическое предложение состоит только из математических и логических терминов или заменяющих их символов.

Определение. Теорема – это математическое предложение, истинность которого доказывается на основе других предложений этой же теории, доказанных ранее, или же аксиом.

Теоремы часто формулируются в виде импликаций. Такая структура наиболее удобна для выделения условия (то, что дано) и заключения (то, что необходимо доказать) теоремы.

Рассмотрим следующую теорему: «Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла». Условием этой теоремы является предложение «Точка лежит на биссектрисе угла», а заключением – предложение «Точка равноудалена от сторон угла». Видим, что и условие, и заключение данной теоремы представляют собой предикаты, заданные на множестве Р всех точек плоскости (см. замечание в § 11 этой главы).

Обозначим через А (х) предикат «Точка х лежит на биссектрисе угла», В (х) предикат «Точка х равноудалена от сторон этого угла», х – это любая точка множества Р. Тогда приведенную теорему можно записать в виде следующей импликации: (" х Î Р) [ А (х) Þ В (х)].

Таким образом, говоря о строении теоремы «Если точка х лежит на биссектрисе угла, то она равноудалена от сторон этого угла», мы выделили в ней три части:

1. Условие теоремы: предикат А (х), заданный на множестве Р всех точек плоскости.

2. Заключение теоремы: предикат В (х), заданный на множестве Р всех точек плоскости.

3. Разъяснительная часть теоремы: в ней описываются множества объектов, о которых идет речь в теореме. В символической записи (" х Î Р).

Заметим, что в словесной формулировке разъяснительная часть обычно опускается, но она всегда подразумевается, и при работе с теоремами ее необходимо выделять. Заметим, что условие и заключение теоремы в свою очередь может не быть элементарным высказыванием, а иметь определенную логическую структуру (чаще всего это конъюнкция или дизъюнкция).

Часто теорема выражается в категорической форме. Например: «синус является нечетной функцией». Но и такая теорема может быть выражена в так называемой условной форме, т.е. в виде «если …, то …».

Теоремы, не содержащие слов «если..., то …», также могут быть записаны в виде импликации. Например, рассмотрим теорему «В прямоугольном треугольнике квадрат длины гипотенузы с равен сумме квадратов длин его катетов а, в». В ней утверждается, что если среди различных треугольников выбрать любой прямоугольный, то в нем окажется, что с ² = а ² + в ². Обозначив множество всех треугольников на плоскости буквой X, а любой треугольник из этого множества буквой х, получим символическую запись теоремы, о которой идет речь,

(" х Î Х) [ А (х) Þ В (х)],

где А (х) предикат «Треугольник х – прямоугольный», В (х) предикат «Квадрат длины гипотенузы равен сумме квадратов катетов (с ² = а ² +
+ в ²)», заданных на множестве X.

Пусть (" х Î Х) [ А (х) Þ В (х)] символическая запись некоторой теоремы. Тогда ее условие и заключение образуют импликацию, истинную при всех х из множества X, и, следовательно, предикат В (х) логически следует из предиката А (х). Поэтому В (х) (заключение теоремы) является необходимым условием для А (х) (условия теоремы), а А (х) – достаточным условием для заключения теоремы В (х).

Пользуясь терминами «необходимое условие» и «достаточное условие», теорему Пифагора можно прочитать следующим образом:

1. Для того, чтобы треугольник был прямоугольным, необходимо, чтобы с ² = а ² + в ²;

2. Для того, чтобы с ² = а ² + в ², достаточно, чтобы треугольник был прямоугольным.