Между понятиями существуют отношения, отражающие связи соответствующих понятиям множеств объектов. Важнейшей формой связи понятий является их родо-видовое подчинение, которое складывается при формировании понятий и обнаруживается там и тогда, где и когда имеет место непосредственная преемственность в переходах от одних понятий к другим. Например, объединение понятий «сложение», «вычитание», «умножение» и «деление» есть понятие «арифметическое действие». Оно будет подчинять четыре предыдущих понятия как видовые и станет для них родовым. На базе понятий (видовых) «арифметическое действие», «возведение в степень» и «извлечение корня» образуется новое (родовое) понятие «алгебраическая операция», с которым связаны такие понятия, как «алгебраическое выражение», «алгебраическая функция», «алгебраическое уравнение».
На кругах Эйлера каждое родо-видовое отношение понятий, из которых В – вид, Р – род, изображается так (рис. 1):
 |
Р
В
Понятие Р является ближайшим для вида В.
Не всегда легко и однозначно можно определить ближайший род. Если между зависимыми понятиями нельзя поставить еще одно понятие, будем иметь отношения ближайшего рода и вида.
Так между понятиями «прямоугольник» и «четырехугольник» можно поставить понятие «параллелограмм», поэтому ближайшим родом для понятия «прямоугольник» является понятие «параллелограмм». Для понятия «квадрат» имеется два ближайших понятия: «прямоугольник» и «ромб» (проиллюстрируйте самостоятельно этот факт на кругах Эйлера).
Существуют и другие отношения между понятиями.
Сравнимые (имеющие общие свойства) и несравнимые (когда нет общих свойств). Например, треугольник, квадрат и круг – сравнимые понятия (Почему?). Треугольник и дробь – несравнимые. Сравнимые понятия могут быть совместимыми и несовместимыми, в зависимости от того пересекаются их объемы или нет.
Совместимые понятия могут быть равнозначными (полупрямая и луч), пересекающимися (целое число и положительное число).
Определение понятий
Любая наука, в том числе и математика, ставит вопросы типа: «Что это такое?» На этот вопрос отвечают определения понятий. Например, что такое клетка? – в биологии, что такое материя? – в философии, что такое пирамида? – в геометрии. Определением принято называть предложение, в котором разъясняется смысл понятия.
Чтобы определить понятие, нужно совершить некоторую логическую операцию, в результате которой будет сформулировано предложение, в котором должно быть в краткой и четкой форме изложено то, что единственным образом характеризует данный предмет, явление и т.д. Существуют различные способы определения понятий. Прежде всего, различают явные и неявные способы. Ниже приведены способы определения понятий и примеры.
1. Через род и видовое отличие. Такое определение можно представить в виде следующей схемы:
Схема 1
Например, параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны. Квадрат – это прямоугольник с равными сторонами.
2. Генетическое определение. Такое определение отличается от первого способа тем, что вместо видового отличия указывают способ получения объекта. Например, четное число – это число, которое делится на два; треугольник – это фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, их соединяющих.
3. Индуктивное определение объединяет следующие три пункта: 1) перечисляются элементарные объекты, принадлежащие объему определяемого понятия; 2) формулируются правила образования новых объектов из уже имеющихся и 3) утверждается, что других объектов, принадлежащих объему определяемого понятия, кроме тех, которые могут быть образованы в соответствии с первыми двумя пунктами определения, нет. Например, индуктивное определение числового выражения таково: 1) каждое число считают числовым выражением; 2) новые числовые выражения могут быть образованы из числовых выражений А и В, если соединить их знаками действий (операций) и 3) других числовых выражений, кроме тех, которые могут быть образованы в соответствии с первыми двумя пунктами определения, нет.
4. Контекстуальное определение. В нем содержание нового понятия раскрывается через отрывок текста, через контекст. Таким образом, например, нами было введено понятие «множество». Таким образом вводится понятие уравнения и его решения в начальной школе.
5. Остенсивное определение. Такое определение раскрывает содержание нового понятия путем показа (демонстрации) определяемого объекта. Например, таким образом определяются в начальной школе понятия числовых равенств и неравенств. Таким образом можно дать определение линейной функции: функция вида f (x) = kx + в, где k и в – числа, называется линейной функцией.
6. Определение-соглашение. Этим термином обозначаются такие определения, в которых раскрывается смысл новых обозначений, символов, не укладывающихся в рамках обычных, ранее известных случаев. Например, принято считать а 0 = 1. Вот еще одно известное определение: под произведением двух дробей 
и 
понимают дробь вида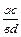 
.
7. Перечисление объектов, входящих в объем понятия. Например, единицы, десятки, сотни составляют класс единиц; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – однозначные числа.
8. Аксиоматическое определение. Это неявное определение, так как оно прямо не называет класс объектов, который описывается с помощью аксиом. В математике существует аксиоматическое определение целого неотрицательного числа, аксиоматическое определение величины и др.
