РАЗЛИЧНЫХ ФОРМ ДВИЖЕНИЯ И ВЗАИМОДЕЙСТВИЯ ТЕЛ.
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
Энергия, работа, мощность
Энергия - универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
 Если тело движется прямолинейно и на него действует постоянная сила
Если тело движется прямолинейно и на него действует постоянная сила  , которая составляет некоторый угол ά с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = F cosά), умноженной на перемещение точки приложения силы:
, которая составляет некоторый угол ά с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = F cosά), умноженной на перемещение точки приложения силы:
A = Fs s = Fs cosά. (3.1)
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (3.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение  , то силу
, то силу  можно считать постоянной, а движение точки ее приложения - прямолинейным. Элементарной работой силы
можно считать постоянной, а движение точки ее приложения - прямолинейным. Элементарной работой силы  на перемещении
на перемещении  называется скалярная величина
называется скалярная величина
dА = 
 = F cosά · ds = F s ds,
= F cosά · ds = F s ds,
где ά - угол между векторами  и
и  ; ds = |
; ds = |  | — элементарный путь; F s - проекция вектора
| — элементарный путь; F s - проекция вектора  на вектор
на вектор  (рис. 3.1).
(рис. 3.1).
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
A =  . (3.2)
. (3.2)
Для вычисления этого интеграла надо знать зависимость силы F s от пути s вдоль тра 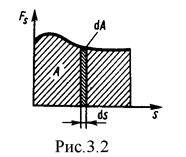 ектории 1-2. Пусть эта зависимость представлена графически (рис. 2), тогда искомая работа А определяется на графике площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F = const и ά = const, то получим
ектории 1-2. Пусть эта зависимость представлена графически (рис. 2), тогда искомая работа А определяется на графике площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F = const и ά = const, то получим
А =  ,
,
где s - пройденный телом путь (см. также формулу (3.1)).
Из формулы (3.1) следует, что при ά < π/2 работа силы положительна, в этом случае составляющая  s совпадает по направлению с вектором скорости движения
s совпадает по направлению с вектором скорости движения  (см. рис. 3.1). Если ά > π/2, то работа силы отрицательна. При ά = π/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.
(см. рис. 3.1). Если ά > π/2, то работа силы отрицательна. При ά = π/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.
Единица работы- джоуль (Дж): 1 Дж - работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н·м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
N =  (3.4)
(3.4)
За время Δ t сила  совершает работу
совершает работу 
 , а мощность N, развиваемая этой силой, в данный момент времени равна
, а мощность N, развиваемая этой силой, в данный момент времени равна
N =  , (3.5)
, (3.5)
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N - величина скалярная.
Единица мощности - ватт (Вт): 1 Вт - мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).






