Для дистанції вибираємо масштаб 1 см = 1 миля, а для швидкостей 1 см = 2 вузли.
З точки, де знаходиться умовно нерухоме судно  , відкладаємо пеленг
, відкладаємо пеленг 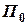 та дистанцію
та дистанцію  і отримуємо точку
і отримуємо точку  , яка вказує початкове положення судна
, яка вказує початкове положення судна  . Повторюємо попередню дію для
. Повторюємо попередню дію для 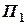 та
та  , це буде точка
, це буде точка  , яка визначає положення судна
, яка визначає положення судна  у момент часу
у момент часу  = 0,1 год. Проведемо з початкового положення судна
= 0,1 год. Проведемо з початкового положення судна  в положення
в положення  напрямлений відрізок і отримуємо вектор переміщення
напрямлений відрізок і отримуємо вектор переміщення  (0,1), що дозволяє отримати вектор відносної швидкості
(0,1), що дозволяє отримати вектор відносної швидкості
 (0,1)/0,1.
(0,1)/0,1.
Вимірювання довжини 
 дає 3,4 см = 3,4 милі, тому
дає 3,4 см = 3,4 милі, тому  = 3,4 / 0,1 = 34 вузли.
= 3,4 / 0,1 = 34 вузли.
Для визначення найкоротшої відстані  , на який розійдуться судна
, на який розійдуться судна  та
та  , проводимо лінію відносного руху (ЛВР) вздовж вектора
, проводимо лінію відносного руху (ЛВР) вздовж вектора  . З точки
. З точки  проводимо перпендикуляр АС до ЛВР (рис. 5.4) і вимірюємо його довжину
проводимо перпендикуляр АС до ЛВР (рис. 5.4) і вимірюємо його довжину
 =3,8 см =3,8 миль.
=3,8 см =3,8 миль.
Вимірюємо шлях, який проходить у відносному русі судно  на момент розходження
на момент розходження  = 12,2 см = 12,2 миль і визначаємо час розходження суден
= 12,2 см = 12,2 миль і визначаємо час розходження суден
 = 0,36 год. = 21,5 хв.
= 0,36 год. = 21,5 хв.
З точки  у вибраному масштабі будуємо вектор абсолютної швидкості судна
у вибраному масштабі будуємо вектор абсолютної швидкості судна  – проведемо промінь за курсом
– проведемо промінь за курсом  = 42° та на ньому відкладемо величину швидкості судна
= 42° та на ньому відкладемо величину швидкості судна  . Оскільки
. Оскільки  , то переносимо вектор
, то переносимо вектор  в кінець вектора
в кінець вектора  і знаходимо вектор
і знаходимо вектор 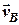 абсолютної швидкості судна
абсолютної швидкості судна  , з’єднавши початкове положення судна
, з’єднавши початкове положення судна  з кінцем перенесеного вектора
з кінцем перенесеного вектора  .
.
Вимірюємо величину швидкості  = 15, 3 см = 30,6 вузлів та його курс
= 15, 3 см = 30,6 вузлів та його курс
 = 326°.
= 326°.
Щоб знайти положення суден на момент розходження визначаємо шлях, який на даний момент пройшло кожне судно
 =
=  =8,64 миль,
=8,64 миль,
 =
=  =11,01 миль,
=11,01 миль,
відкладаємо їх від точок  та
та  (рис. 5.4) і знаходимо положення кожного судна на схемі абсолютного руху на момент розходження.
(рис. 5.4) і знаходимо положення кожного судна на схемі абсолютного руху на момент розходження.
Перевіряємо отриманий результат для мінімальної відстані  між суднами
між суднами  та
та  у абсолютній системі координат на момент розходження.
у абсолютній системі координат на момент розходження.
 б) аналітичний метод
б) аналітичний метод
Положення судна  на моменти часу
на моменти часу  та
та  задано у навігаційній (модифікованій полярній) системі координат, початок якої розташований на судні
задано у навігаційній (модифікованій полярній) системі координат, початок якої розташований на судні  .
.
Перейдемо від навігаційної до декартової системи координат. Тоді положення судна  (цілі) на момент часу
(цілі) на момент часу  = 0 та
= 0 та  = 0,1 (год) буде:
= 0,1 (год) буде:
 = 12,8 sin 120º = 11,1 миль,
= 12,8 sin 120º = 11,1 миль,
 = 12,8 cos 120º = – 6,40 миль,
= 12,8 cos 120º = – 6,40 миль,
 миль,
миль,
 миль,
миль,
Отримані дані дозволяють визначити складові відносної швидкості
 = – 33,3 вуз,
= – 33,3 вуз,
 7,6 вуз.
7,6 вуз.
Отже, вектор відносної швидкості дорівнює
 ,
,
а його модуль
 = 34,2 вуз.
= 34,2 вуз.
Вектор швидкості судна  (спостерігача)
(спостерігача)
 ,
,
Для вектора швидкості судна  отримуємо
отримуємо
 =
=  .
.
Звідки отримуємо його величину
 вуз,
вуз,
та напрям
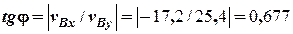
тоді  .
.
Тоді для курсу судна  отримуємо
отримуємо 
Найкоротша відстань між суднами визначиться віддаллю від точки А (0,0) до ЛВР, тому
 ,
,
де  = 7,6 / (–33,3) = – 0,228. Підставляючи значення, знаходимо
= 7,6 / (–33,3) = – 0,228. Підставляючи значення, знаходимо
 =3,77 миль.
=3,77 миль.
Для знаходження моменту розходження, розраховуємо відстань 
 = 12,2 милі
= 12,2 милі
і ділимо її на модуль відносної швидкості
 =12,2 /34,2 = 0,36 год. (27)
=12,2 /34,2 = 0,36 год. (27)
Відповідь: 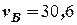 вузлів,
вузлів,  ,
,  = 3,8 миль,
= 3,8 миль,
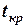 = 0,36 години = 21,5 хв.
= 0,36 години = 21,5 хв.






