Судно рухається відносно води зі сталою швидкістю 
в області течії, курс якої 
і модуль швидкості 
лишаються незмінними. Знайти модуль абсолютної швидкості судна 
та істинний курс 
, якщо судно повинно рухатись заданим напрямом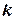 
. Вихідні дані наведені в таблиці СП.5.
Розв’язати задачу графічно (в масштабі 1 см = 2 вузли) та аналітично.
Таблиця СП.5 – вихідні дані для виконання задачі СП.5.
| № | , вуз.
| , вуз.
| 
| 
| № | , вуз.
| , вуз.
|
| .
| |
| 1,8 | 1,8 | |||||||||
| 2,4 | 2,0 | |||||||||
| 2,2 | 2,2 | |||||||||
| 2,6 | 2,6 | |||||||||
| 2,6 | 2,4 | |||||||||
| 2,2 | 2,2 | |||||||||
| 1,6 | 2,2 | |||||||||
| 2,4 | 2,4 | |||||||||
| 2,4 | 2,2 | |||||||||
| 2,4 | 2,0 | |||||||||
| 1,6 | 2,6 | |||||||||
| 2,4 | 2,4 | |||||||||
| 2,2 | 2,6 | |||||||||
| 2,2 | 2,6 | |||||||||
| 2,2 | 1,8 |
Задача двох тіл. Розходження суден
Розглянемо задачу розходження двох суден 
і 
. В модельній задачі розглядаючи рух суден, будемо вважати їх точковими, тобто нехтувати розмірами кожного судна.
Можливі дві задачі:
пряма – відомо положення судна відносно судна у момент часу 
та їх вектори абсолютної швидкості 
та 
. Якщо їх курси перетинаються, то потрібно знайти мінімальну відстань між суднами та момент часу, коли це відбудеться;
обернена – з судна , яке рухається з відомою швидкістю, визначають послідовні положення іншого судна у початковий момент часу та через 0,1 год. Якщо відстань до судна зменшується, то потрібно знайти мінімальну відстань між суднами, момент часу, коли це відбудеться та абсолютну швидкість судна В.
Пряма задача розходження суден
Методика розв’язання прямої задачі
А) Абсолютний рух
Графічно – побудуємо схему руху суден та .
Вказуємо положення суден через 0,1, 0,2, 0,3 і т.д. годин.
По зміні пеленгу суден визначаємо схему розходження.
Аналітично – вводимо нерухому декартову систему координат, помістивши початок координат у початкове положення судна , та визначаємо координати положення суден у довільний момент часу 
.
Розраховуємо відстані між ними у довільний момент часу.
З умови мінімуму відстані знаходимо час розходження та найкоротшу відстань.
Б) Відносний рух
Графічно – будуємо схему руху суден. Переходимо у рухому систему координат, яка жорстко зв’язана з судном , тоді швидкість відносного руху судна буде
.
Будуємо вектор швидкість 
і вздовж нього проводимо лінію відносного руху. Довжина перпендикуляра, опущено з точки на неї, визначає найкоротшу відстань при розходженні.
Вимірюємо величину швидкості відносного руху та пройдений судном шлях до точки розходження і знаходимо час розходження.
Аналітично – записуємо вирази для векторів швидкості суден, знаходимо вектор відносної швидкості
.
Записуємо рівняння лінії відносного руху, яка проходить через точку вздовж вектора 
і розрахуємо відстань точки від неї, яка визначає найкоротшу відстань при розходженні.
Розраховуємо модуль відносної швидкості 
і довжину шляху до моменту розходження, що дозволяє визначити час розходження.
Приклад. В заданий момент часу 
за допомогою радара, що знаходиться, наприклад, на судні , визначено віддаль 
= 9,4 милі та пеленг 
= 62° судна (горизонтальний кут між 
та напрямом на судно , виміряним за стрілкою годинника). Курси суден 
= 18° і 
= 306° (горизонтальний кут між північною частиною меридіана – нордом та відповідним вектором швидкості, виміряним за стрілкою годинника) та швидкості 
= 16 вузлів та 
= 17 вузлів і 
відомі та залишаються незмінними.
Якщо курси суден перетинаються, то потрібно визначити найменшу відстань між суднами 
, а також момент часу, у який це відбудеться?
Спочатку обмежимося розглядом абсолютного руху двох тіл, а потім зведемо задачу до відносного руху.
В модельній задачі розглядаючи рух суден, будемо вважати їх точковими, тобто нехтувати розмірами кожного судна.
1. Метод абсолютного руху суден
В абсолютній (нерухомій відносно поверхні Землі) системі відліку введемо декартову систему координат 
. Її початок сумістимо з судном та направимо вісь 
горизонтально, а вісь 
на північ вздовж меридіана (по норду ).
Перш за все графічно визначимо схему розходження суден. По заданому пеленгу (відкладеному від норду за стрілкою годинника) з точки проводимо промінь та у вибраному масштабі (наприклад, 1 см = 1 миля), відкладаємо на ньому величину 
і знаходимо початкове положення судна (рис. 4.1). З точок і по заданим курсам 
та 
проводимо промені та отримуємо траєкторії 
та 
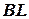абсолютного руху суден (рис. 4.1). Оскільки траєкторії перетинаються, то потрібно розв’язувати задачу на розходження.
За відомими значеннями швидкостей, визначаємо шлях, яке проходить кожне судно за 
= 6 хв. = 0,1 год (
= 1,6 см та 
= 1,7 см), 
= 12 хв. = 0,2 год. ( = 3,2 см та = 3,4 см), та 
= 18 хв. = 0,3 год. ( = 4,8 см та = 5,1 см), і на траєкторіях абсолютного руху суден та 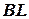позначаємо відповідні положення суден через проміжки часу , та (рис. 2.4).
Вимірюємо відстані між суднами та пеленги судна у ці моменти часу і отримуємо: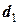 
= 7,5 милі, 
= 5,8 милі та 
= 3,9 милі. 
= 59° , 
= 54° та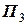 
= 44°. Зміна пеленга судна означає, що судна та розійдуться. Оскільки судно знаходиться праворуч, а його пеленг зменшується <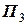 
, то у даній задачі судно проходить перед судном (по носу судна ). Якби при даному початковому розташування суден зміна пеленгу була зворотною, то судно проходило би перед судном (по носу судна ).
Тепер визначимо аналітично найкоротшу відстань при розходженні та момент часу, коли воно відбудеться. Рівняння абсолютного руху кожного судна мають вигляд:
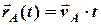, (1)
(2)
де вектори 
, 
задані своїми напрямами та чисельними значеннями та 
.
Тоді з рівнянь (1) та (2) визначаємо координати суден та у довільний момент часу :
, (3)
, (4)
, (5)
, (6)
(всі віддалі в милях, а швидкості у вузлах).
З системи рівнянь (3) – (6) розраховуємо у довільний момент часу відстань 
між судном та і пеленг 
судна за формулами:
= 
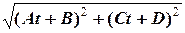, (7)
= 
, (8)
в яких:
= – 18,69 вуз., (9)
= – 5,22 вуз., (10)
= 8,30 милі, (11)
= 4,41 милі. (12)
З формул (3) – (6) у моменти часу 
, 
та знаходимо координати кожного судна (милі) та пеленг судна В:
= 0,49, 
= 1,52, 
= 6,92, 
= 5,41, 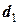= 7,52, = 58,3° ;
= 0,99, 
= 3,04, 
= 5,55, 
= 6,41, = 5,67, = 53,6°.
= 1,48, 
= 4,57, 
= 4,17, 
= 7,41, = 3,92, 
= 43,4°,
що підтверджує результати, які ми отримали з рис. 4.1, визначаючи схему розходження.
Розраховуємо відстань між суднами і будуємо залежність , яка зображена на рис. 4.2. З графіка видно, що величина відстані між суднами змінюється не монотонно. Мінімум кривої дозволяє визначити найменшу відстань між суднами 
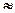2 милі та момент часу 
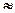0,47 год 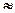28 хв., коли це відбудеться.
Аналітично найменшу віддаль між суднами знаходимо з умови рівності нулю похідної: 
, що згідно рівнянню (7) дає
, (13)
звідки визначаємо час , коли судна розійдуться на найменшій відстані
. (14)
Для визначення необхідно підставити значення у вираз для , що після алгебраїчних перетворень дає
(15)
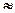З урахуванням даних задачі, з формул (14) та (15) отримуємо: = 0,47 год. 28 хв., = 2,0 милі, що підтверджує дані, які визначили, розв’язуючи задачу графічним методом.
Час розходження = 0,47 год. дозволяють визначити координати (в милях) кожного судна у цей момент:
, 
,
= 2,20, 
= 9,11.
Положення суден та у момент розходження (точки 
та 
на їх траєкторіях абсолютного руху) та відстань між ними вказані на рис. 4.1.
