Складний рух точки
Рух судна в області дії постійної течії
Судно рухається зі швидкістю 
відносно води в області, де діє течія, вектор швидкості 
якої незмінний та відомий (величина 
та напрям 
).
Виникають 2 задачі: пряма – визначити величину абсолютної швидкості і на скільки течія змінить курс 
, яким рухається судно.
обернена – визначити величину абсолютної швидкості та курс , який потрібно тримати по компасу, щоб судно рухалося заданим шляховим кутом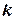 
в області дії відомої сталої течії.
Пряма задача руху судна в області дії постійної течії
Методика розв’язання прямої задачі
Оскільки відомий вектор швидкості судна 
відносно води (величина відносної швидкості та курс ) та вектор швидкості течії 
, яка відіграє роль переносної швидкості, то абсолютну швидкість руху судна знаходимо шляхом складання векторів
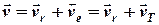
Графічно розв’язуємо задачу шляхом складання векторів та .
З початкової точки будуємо вектор швидкості судна – знаходимо місце, куди може попасти судно у відсутності переносного руху, а потім до кінця вектора додаємо вектор швидкості переносного руху . Або навпаки спочатку будуємо , а потім . Визначаємо модуль та напрям абсолютної швидкості.
Аналітично – вводимо декартову систему, записуємо вирази для векторів та через проекції на ці вісі координат. Знаходимо вектор абсолютної швидкості і розраховуємо його модуль та напрям.
Приклад. Знайти абсолютну швидкість 
судна (модуль 
та шляховий кут 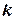), якщо відомі вектор швидкості течії 
(
= 80°, 
= 3 вузли) та вектор відносної швидкості судна 
(
= 40°, 
= 16 вузлів).
Розв’язання.
Графічний метод розв’язання прямої задачі зводиться до геометричної побудови суми векторів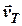 
і та відповідних вимірювань.
Будемо працювати у масштабі мапи для швидкості 1 см = 2 вузла та для відстані 1 см = 2 милі. Помітимо початкове положення судна (точка 
) і з цієї точки проведемо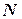 
-норд (рис. 3.1). Від нього за напрямом руху стрілки годинника відкладаємо кут , проводимо промінь на якому відкладаємо модуль вектора течії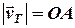 
(умовно відключаємо двигун і визначаємо, що під дією тільки течії судно за одну годину опинилося би у точці 
).
Після цього умовно відключаємо течію і визначаємо, куди з точки за одну годину прийде судно рухаючись відносно води зі швидкістю . Для цього з кінця вектора (точки ) від проведеного норду 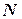відкладаємо кут , проводимо промінь і на отриманій лінії відкладаємо модуль вектора 
. З’єднаємо точки і 
та отримаємо вектор абсолютної швидкості 
, який визначає величину 
абсолютної швидкості та шляховий кут 
.
Вимірювання довжини вектора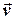 
дає абсолютну швидкість судна = 
= 18,4 вузлів. Шляховий кут = 46° і кут зносу 
= 6° вимірюються безпосередньо на рис. 3.1.
Аналітичний метод базується на тому, що відомі обидві складові абсолютної швидкості – вектори 
і . Вводимо декартову систему координат, помістивши початок у точку . Спрямуємо вісь 
горизонтально, а вісь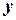 
– вертикально (по норду), тоді для векторів та (рис. 3.1) отримуємо:
= 
,
= 
.
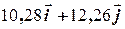Дістаємо
= 
.
Отож:
= 13,17 (вуз.), 
= 12,78 (вуз.),
звідки послідовно знаходимо:
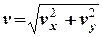= 18,4 (вуз.),
= 1,031,
і, відповідно,
(1,031) = 46°.
Відповідь: 
= 18,4 вузлів, 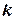=46°.
Задача СП.4. Рух судна в області дії постійної течії – пряма задача
Судно рухається відносно води зі сталою швидкістю 
в області течії, курс якої і модуль швидкості лишаються незмінними. Знайти вектор абсолютної швидкості судна - його модуль 
та шляховий кут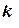 
, якщо істинний курс заданий і лишається незмінним. Вихідні дані наведені в таблиці СП.4.
Розв’язати задачу графічно (в масштабі 1 см = 2 вузли) та аналітично.
Таблиця СП.4 – вихідні дані для виконання задачі СП.4.
| № | , вуз.
| , вуз.
| 
| 
| № | , вуз.
| , вуз.
|
|
| |
| 2,2 | 1,6 | |||||||||
| 2,6 | 1,8 | |||||||||
| 2,4 | 2,4 | |||||||||
| 2,2 | 2,2 | |||||||||
| 1,8 | 2,4 | |||||||||
| 2,4 | 2,6 | |||||||||
| 2,2 | 2,6 | |||||||||
| 2,0 | 2,2 | |||||||||
| 2,2 | 2,4 | |||||||||
| 2,0 | 2,4 | |||||||||
| 2,6 | 2,2 | |||||||||
| 2,4 | 2,2 | |||||||||
| 2,6 | 2,4 | |||||||||
| 1,8 | 2,2 | |||||||||
| 2,6 | 1,6 |
