Зная вид функции, выражающей потенциальную энергию системы, можно сделать ряд заключений о характере поведения системы. Особенно наглядно это можно сделать в случае одномерного движения тела, т. е. движения, описываемого одной координатой (например, координатой х). График зависимости потенциальной энергии от аргумента U = U (x) называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.
Будем рассматривать только консервативные системы, т. е. системы, в которых превращения механической энергии в другие виды энергии отсутствуют, т. е. когда справедлив закон сохранения энергии.
Из анализа графика на рис. 18 приходим к выводу, что при полной энергии тела, равной Е, тело не может сместиться правее х 2 и левее х 1, так как кинетическая энергия K не может быть отрицательной величиной и, следовательно, потенциальная энергия U не может быть больше полной. В таком случае говорят, что тело находится в потенциальной яме с координатами х 1£ х £ х 2.
В точке с координатой х 0 потенциальная энергия частицы минимальна. В этой точке действующая на частицу сила F x = - d U /d x = 0. При смещении частицы из положения х 0 влево или вправо на нее действует возвращающая сила. Поэтому положение х 0 является положением устойчивого равновесия.
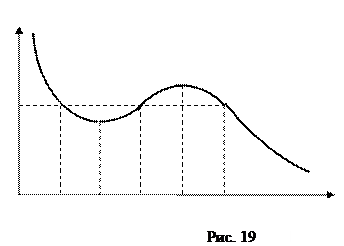
В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рисунок 19). Проанализируем эту потенциальную кривую. Если Е - заданная полная энергия частицы, то частица может находиться только там, где U (x) £ E, т. е. в областях I (х 1 £ х £ х 2) и III (х ³ х 3).
Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер в области II (х 2 £ х £ х 3), ширина которого равна интервалу значений х, при которых Е < U, а высота – определяется разностью (U max – Е).Для того, чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме и совершает колебания между точками с координатами x 1 и x 2.
 |
I II III
В точке с координатой x 0 (рис. 19) потенциальная энергия частицы минимальна. Так как действующая на частицу сила F x = - d U /d x (U - функция только одной координаты), а условие минимума потенциальной энергии d U /d x = 0, то в точке с координатой x 0 сила Fx (x 0) = 0. При смещении частицы из положения x 0 (и влево, и вправо) она испытывает действие возвращающей силы, поэтому положение x 0 является положением устойчивого равновесия. Указанные условия выполняются и для точки x 0¢ (для U max). Однако эта точка соответствует положению неустойчивого равновесия,так как при смещении частицы из положения x 0¢ появляется сила, стремящаяся отклонить ее от этого положения.
Движение тел с переменной массой*
Вклассической механике масса движущегося тела может изменяться лишь вследствие присоединения к телу или отделения от него материальных частиц или частей тела. В результате этого
.
Уравнение поступательного движения тела переменной массы (уравнение Мещерского) имеет вид:
, (2.2.7)
где m,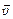 
– масса и скорость тела в рассматриваемый момент времени,
– результирующая внешняя сила,
– скорость отделяющихся частиц (частей) после отделения (если 
), или присоединяющихся частиц до присоединения (если 
),
– относительная скорость отделяющихся или присоединяющихся частиц, т.е. их скорость относительно тела.
Реактивная сила
. (2.2.8)
В случае движения ракеты, когд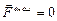а 
, а 
, связь между скоростью ракеты и ее массой выражается формулой Циолковского:
, (2.2.9)
где m 0 – начальная масса ракеты.
Из формулы Циолковского ясно, что, чем больше скорость истечения газов реактивной струи ракетного двигателя относительно ракеты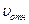 
, тем большую скорость может приобрести ракета.
Максимальная (характеристическая) скорость ракеты равна:
, (2.2.10)
где 
– начальная масса топлива.
Реактивное движение
Реактивным называется движение с изменяющейся массой.
Рассмотрим движение ракеты. Пусть в момент времени t масса ракеты m (t) и скорость 
. Импульс ракеты 
. Через промежуток времени d t масса ракеты изменилась и стала (m‑ d m), скорость 
, количество движения 
Также надо учесть количество движения порции газа 
. Приращение количества движения равно импульсу внешней силы:
,
учтем добавочное условие d m = d m газ. Раскрывая скобки, имеем:
.
Пренебрегая членом второго порядка малости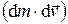 
и учитывая добавочное условие d m = d m газ, имеем 
. Окончательно получаем уравнение Мещерского:
,
в этом уравнении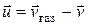 
, скорость истечения струи газа относительно ракеты.
Если представить ракету и струю газа как замкнутую систему, то получим уравнение Циолковского
.
Это уравнение легко решается в предположении, что скорость газа и скорость ракеты направлены вдоль одной прямой в противоположных направлениях, т. е.: 
.
В этом случае
; 
.
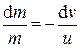Константа определяется из начальных условий: при t = 0, v = 0, m = m 0.
.
Последнее соотношение позволяет оценить запас топлива, необходимый для достижения заданной скорости.
