Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами методами операционного исчисления

Пусть требуется проинтегрировать уравнение

при начальных условиях:

- заданные постоянные, а - заданная функция, изображаемая по Лапласу.

Обозначим изображение искомого решения через .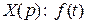

По теореме дифференцирования оригинала (3.4.2), в силу заданных начальных условий имеем:

.

Пусть, далее, .

Подставляя в исходное уравнение вместо функций их изображения, получаем так называемое изображающее уравнение:

(здесь ),

т.е. – алгебраическим относительно изображения искомого решения

.

Для отыскания решения остается по полученному изображению найти его оригинал, пользуясь известными теоремами.

Рассмотрим несколько примеров решения задачи Коши методами операционного исчисления.

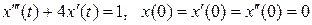
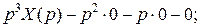1.

1 .

, = −

.

3.

Зная: 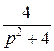и , получим

. Отсюда .

Оригиналы для изображений и 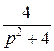известны, а именно:

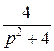
, .Оригинал найдем по теореме свертывания:

Окончательно:

 

Изображение периодической функции

В заключение, приведём ещё один пример построения изображения.

Пусть требуется найти изображение периодической функции с периодом (при ). (При (3.3)).

 

 

 

Введем вспомогательную функцию , которая на полуотрезке равна , вне этого отрезка равна 0, т.е.

.

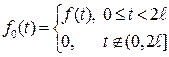Ее изображением будет служить функция 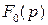, определяемая следующим образом:

,

.

Функцию , в свою очередь, можно выразить через следующим образом: , здесь 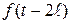- та же периодическая функция, но с запаздыванием на один период, равная нулю при 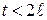. Переходя в последнем равенстве к изображениям и используя теорему запаздывания (3.5.2), получаем: , откуда: .

Таким образом, изображение периодической функции с периодом определяется следующими формулами:

, где .

Пример. В качестве примера найдем изображение функции .

 

 

 

Отсюда: .

 

Вопросы для самопроверки.

1. Для всякого ли оригинала существует изображение ? Сформулировать требования к оригиналу.
2. Как изменится изображение, если аргумент оригинала умножить на а = 3?
3. Решить систему дифференциальных уравнений

4. Найти оригинал изображения , применив третью теорему разложения (пункт 3.6.3).

 

 

Л И Т Е Р А Т У Р А

Основная литература

1. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1966.-331с.

2. Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Учебник для вузов (под ред. В.С.Зарубина и А.П. Крищенко). – М.: МГТУ, –1996. (Серия «Математика в техническом университете», вып. XI).

3. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задача и упражнения. – М.: Наука, 1981. – 215с.

4. Сборник задач по математике для втузов. Специальные разделы математического анализа. Под ред.Ефимова А.В., Демидовича Б.П., т.2. – 2-е изд. - М.: Наука, 1986.-368с.

Дополнительная литература

1. Мышкис А.Д. Математика для втузов. Специальные курсы. – М.: Наука, 1971. – 632с.

2. Смирнов В.И. Курс высшей математики. Т.2. – М.: ГИФМЛ, 1961. – 628с.

3. Шостак Р.Я. Операционное исчисление. М.: Высшая школа. – 1972. - 252с.

Методические и учебные пособия

1. Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы студентов по разделам «Теория функций комплексного переменного» и «Операционное исчисление». – М.: МВТУ,1988.-28с.

2. Шостак Р.Я. Учебное пособие по операционному исчислению. – М.: МВТУ, 1967. – 100с.