Теорема подобия
Пусть 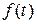

 и
и  . В этом случае
. В этом случае 
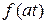

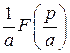 . (3.1.) Доказательство.
. (3.1.) Доказательство. 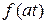

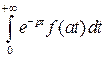 . Сделаем замену:
. Сделаем замену: 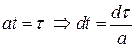
тогда 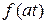

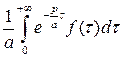 , или
, или 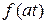

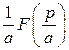 .
.
Из формулы (3.1) следует, что увеличению независимой переменной оригинала в 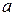 раз,
раз,
соответствует уменьшение в 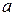 раз как независимой переменной изображения, так и самого изображения.
раз как независимой переменной изображения, так и самого изображения.
Теорема запаздывания
Определение. Функция, 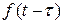 , где
, где 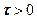 некоторая постоянная величина, называется функцией запаздывающего аргумента (относительно функции
некоторая постоянная величина, называется функцией запаздывающего аргумента (относительно функции  , (рис.3.1)).
, (рис.3.1)).
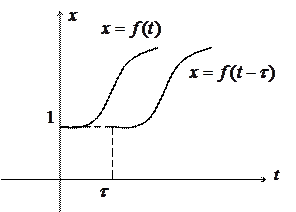 Обозначим функцию
Обозначим функцию 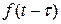 через
через 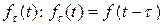 . (Если t − время, то функция
. (Если t − время, то функция 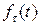 описывает процесс с запаздыванием на время τ)
описывает процесс с запаздыванием на время τ)
Рис. 3.1.
Зная изображение  функции
функции 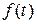 , можно найти изображение
, можно найти изображение 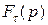 функции
функции 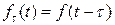 , пользуясь формулой
, пользуясь формулой 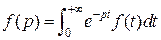 .
.
Так как  , имеем:
, имеем:
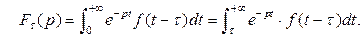
Применяя подстановку 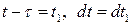 , (при
, (при 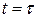 ,
, 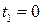 и
и 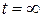 ,
, 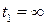 ), имеем
), имеем
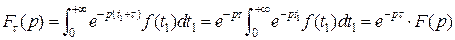 .
.
Таким образом: 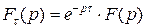 , то есть
, то есть 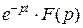

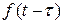
Теорема смещения
Если функция 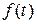 является оригиналом, то при любом вещественном или комплексном
является оригиналом, то при любом вещественном или комплексном 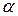 оригиналом будет являться и функция
оригиналом будет являться и функция 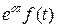 , так как из оценки
, так как из оценки
 вытекает
вытекает 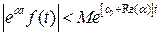 при
при 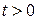 .
.
Найдем изображение этой функции
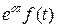

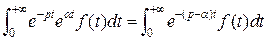 .
.
Интеграл в правой части последнего равенства отличается от интеграла Лапласа, определяющего изображения 

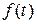 лишь тем, что в последнем аргумент изображения
лишь тем, что в последнем аргумент изображения 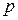 заменен на
заменен на 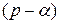 .
.
Таким образом, если 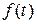

 , то
, то 

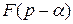 .
.
Пример. 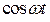

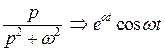

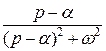
Изображения основных элементарных функций
Приведём таблицу изображений основных элементарных функций, которые были получены в предыдущих разделах в качестве примеров, либо их обобщений. Напомним, что все функции удовлетворяют условиям, сформулированным в пункте 2.1.
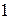

 ,
, 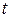
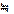
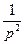 ,
, 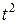
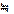
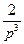 ,
, 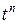
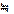
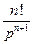 ,
, 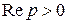
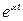

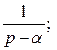
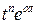

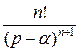
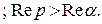
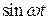

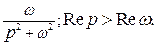
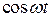

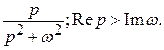
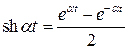

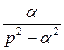 ;
; 

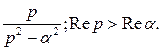
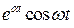

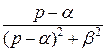 ,
, 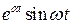

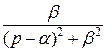 ,
,
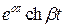

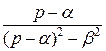 ,
, 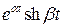

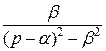
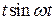

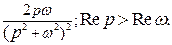
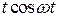

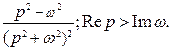


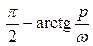
Приведём ещё несколько свойств оригиналов и изображений, используемых как для определения изображений, так и для восстановления оригиналов.
Теорема свертывания
Определение. Сверткой двух функций 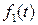 и
и 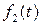 называется функция
называется функция 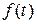 , определяемая формулой
, определяемая формулой 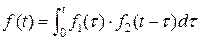 .
.
(Операцию получения свертки часто называют свертыванием двух функций).
Если в интеграле заменить 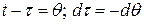 , (
, (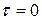 ,
, 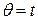 ;
; 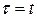 ,
,  ) то формула примет вид:
) то формула примет вид: 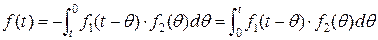
или 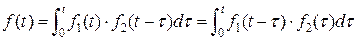 ,
,
т.е. функции 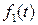 и
и 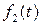 , входящие в свертку, равноправны.
, входящие в свертку, равноправны.
Поставим теперь задачу выразить изображение  свертки
свертки 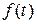 через изображения
через изображения 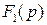 и
и 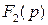 свертываемых функций
свертываемых функций 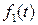 и
и 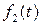 .
.
Теорема. Изображение свертки двух функций равно произведению их изображений.
Если 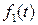

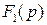 , а
, а 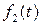

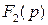 , то
, то 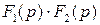

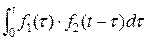 , или
, или 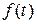

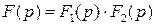 .
.
Доказательство. Определим изображение функции 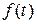 :
:
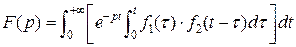 ,
,
Причем областью интегрирования является часть первого координатного угла, ограниченная прямыми 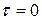 и
и 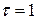 (рис. 4.1).
(рис. 4.1).

Рис. 4.1.
Изменим порядок интегрирования в полученном интеграле.
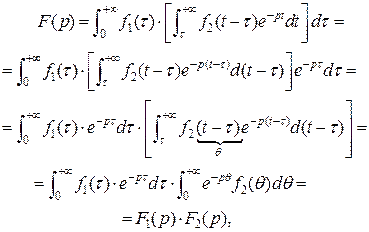
(т.к. 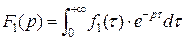 и
и 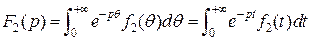 .)
.)
Таким образом, 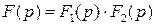 или
или
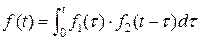

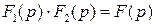
Пример. Найти оригинал 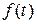 , зная его изображение:
, зная его изображение: 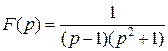 .
.
Решение. Обозначим: 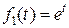

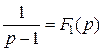 и
и 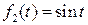

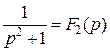 ,
,
По теореме умножения функций 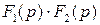

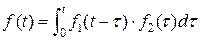
.
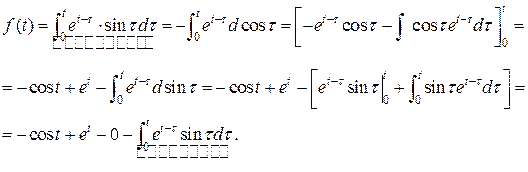
Итак: 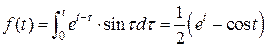 , т.е.
, т.е.
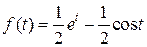

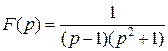 .
.
Проверим:
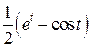

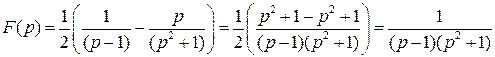 , что и требовалось доказать.
, что и требовалось доказать.
Теоремы разложения
Теоремы разложения применяются для нахождения оригинала 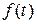 , когда известно изображение
, когда известно изображение  . Каждая из этих теорем справедлива лишь при определенных частных условиях, накладываемых на изображение
. Каждая из этих теорем справедлива лишь при определенных частных условиях, накладываемых на изображение  . Однако классы функций, удовлетворяющих этим условиям, являются весьма широкими; вычисления же, связанные с применением теорем разложения, настолько просты, что использование этих теорем при решении многих конкретных задач оказывается весьма эффективным.
. Однако классы функций, удовлетворяющих этим условиям, являются весьма широкими; вычисления же, связанные с применением теорем разложения, настолько просты, что использование этих теорем при решении многих конкретных задач оказывается весьма эффективным.
Первая теорема разложения
Предположим, что данное изображение  может быть разложено в ряд по степеням
может быть разложено в ряд по степеням  :
:
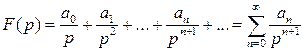 , (5.1)
, (5.1)
сходящийся при 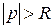 .
.
Если к каждому отдельному члену этого ряда применить операционное соотношение:
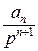

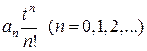 ,
,
то оригинал 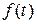 определяется формулой:
определяется формулой:
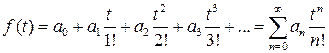 . (5.2)
. (5.2)
Пример. 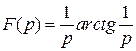 разлагается в ряд:
разлагается в ряд:
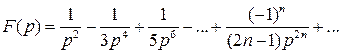
По первой теореме разложения
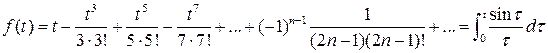 .
.
Вторая теорема разложения
Для того, чтобы найти оригинал функции 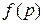 , изображение
, изображение  которой заданно дробно-рациональной функцией
которой заданно дробно-рациональной функцией
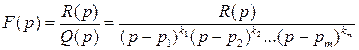 ,
,
(степень числителя меньше степени знаменателя), разлагаем изображение  на элементарные дроби, после чего находим оригинал каждой дроби.
на элементарные дроби, после чего находим оригинал каждой дроби.
Пример. 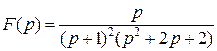

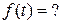
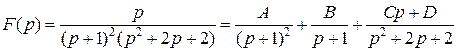 ,
,
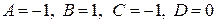 .
.
Получим: 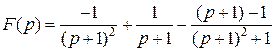 .
.
Запишем оригинал:
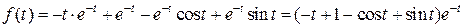 .
.
3.6.3. Третья теорема разложения
Если изображением  искомой функции
искомой функции 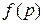 служит функция комплексного аргумента, регулярная справа от прямой
служит функция комплексного аргумента, регулярная справа от прямой 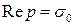 , а на этой прямой и слева от нее не имеющая других особенностей, кроме конечного множества полюсов и существенно особых точек, то оригиналом для этой функции служит функция
, а на этой прямой и слева от нее не имеющая других особенностей, кроме конечного множества полюсов и существенно особых точек, то оригиналом для этой функции служит функция 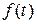 , определяемая по формуле
, определяемая по формуле
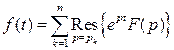 . (5.3)
. (5.3)
Пример. 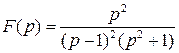

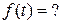
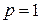 - полюс 2-го порядка,
- полюс 2-го порядка, 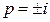 - полюсы 1-го порядка.
- полюсы 1-го порядка.
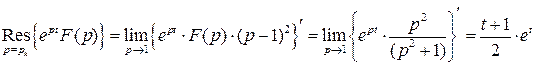 .
.
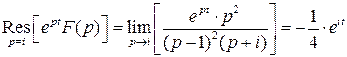 .
.
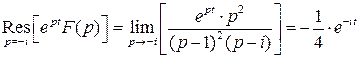 .
.
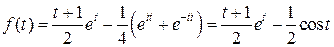 .
.






