Исходной формулой операционного исчисления является формула (3.7):
 ,
,
определяющая преобразование Лапласа. Обычно, эту формулу, связывающую функцию  с функцией f (t), заменяют символической записью
с функцией f (t), заменяют символической записью 

 .
.
Определение. Функцию  называют начальной функцией или оригиналом, а функция
называют начальной функцией или оригиналом, а функция  , получаемую из
, получаемую из  при помощи преобразования Лапласа, называется изображением функции
при помощи преобразования Лапласа, называется изображением функции  .
.
Изображения имеют только те функции, для которых имеет смысл интеграл Лапласа (1.9).
Примером функции, не имеющей изображения, может служить функция 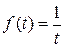 . Точно так же не всякая функция комплексного переменного может рассматриваться как изображение некоторой функции вещественного переменного. Например, не имеет оригинала функция
. Точно так же не всякая функция комплексного переменного может рассматриваться как изображение некоторой функции вещественного переменного. Например, не имеет оригинала функция  , так как полюсы этой функции распределяются по всей вещественной оси. То есть на комплексной плоскости
, так как полюсы этой функции распределяются по всей вещественной оси. То есть на комплексной плоскости 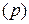 нет ни одной прямой, параллельной мнимой оси, справа от которой эта функция была бы регулярной.
нет ни одной прямой, параллельной мнимой оси, справа от которой эта функция была бы регулярной.
Мы будем рассматривать только такие начальные функции  , которые удовлетворяют трем условиям:
, которые удовлетворяют трем условиям:
1) 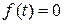 при
при 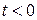 ,
,
2)  при
при 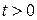 , где
, где 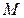 и
и  - некоторые положительные постоянные числа,
- некоторые положительные постоянные числа,
3) На любом конечном отрезке 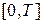
 удовлетворяет условиям Дирихле (п.3.1).
удовлетворяет условиям Дирихле (п.3.1).
Кроме того, всегда будем считать, что в формуле (1.9) 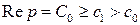 ;
;
При этих условиях интеграл Лапласа, определяющий функцию  , равномерно сходиться во всей полуплоскости, ограниченной прямой
, равномерно сходиться во всей полуплоскости, ограниченной прямой 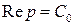 . Функции
. Функции  , удовлетворяющие всем этим условиям, будем называть изображаемыми по Лапласу.
, удовлетворяющие всем этим условиям, будем называть изображаемыми по Лапласу.
Приведём два примера непосредственного вычисления изображений для функций, играющих очень важную роль в операционном исчислении.
1. Функция, равная нулю при 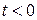 и равная единице при
и равная единице при 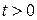 ; эта функция называется единичной функцией и обозначается
; эта функция называется единичной функцией и обозначается  :
:

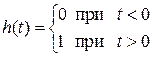 .
.
Изображение 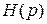 единичной функции
единичной функции  легко определяется по формуле (2.1):
легко определяется по формуле (2.1):
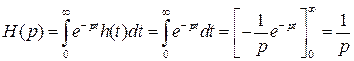 ,
,
Следовательно, 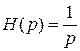 при
при 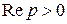 , то есть:
, то есть: 

 .
.
2. Экспоненциальная функция, равная нулю при 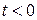 и равная
и равная 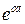 при t > 0:
при t > 0:
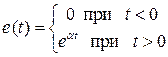 . В дальнейшем будем писать просто
. В дальнейшем будем писать просто 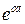 .
.
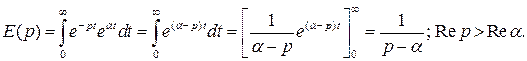
Отсюда 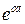

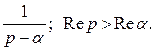
Основные свойства изображений и оригиналов.
Линейность.
1) Умножение начальной функции (оригинала) на постоянную величину влечет за собой умножение на ту же постоянную изображения:
Пусть 

 . В этом случае
. В этом случае 

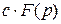 ,
,
Например, 

 , т.к.
, т.к. 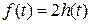 .
.
2) Изображение алгебраической суммы конечного числа начальных функций равно алгебраической сумме изображений этих функций:
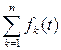

 , где
, где 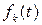

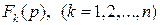 .
.
Два рассмотренных свойства называются линейными и легко объединяются:
Изображение линейной комбинации оригиналов равно той же линейной комбинации соответствующих изображений:
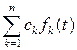

 , где
, где 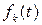

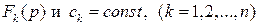 .
.
Доказательство этих свойств основано на применении простейших теорем об определенном интеграле.
Пример. 

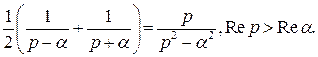
Отсюда сразу получаем: 

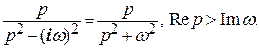
Замечание. При использовании операционного исчисления обычно обращаются к каталогам, содержащим некоторое число оригиналов и их изображений, определенных заранее (вывод некоторых из них будет дан ниже). Ясно, что такие каталоги могут быть использованы и для практического решения обратной задачи, состоящей в определении начальной функции по данному изображению этой функции.




