В дальнейшем при формулировке и доказательстве теорем операционного исчисления мы всегда будем считать, что все рассматриваемые начальные функции:
1) изображаемы по Лапласу;
2) дифференцируемы необходимое количество раз;
3) все производные изображаемы по Лапласу.
Оригинал будем обозначать малыми буквами, а изображения – соответствующими большими буквами (например, 
, 
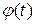
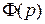и т.д.).
Дифференцирование оригинала
Допустим, что оригинал − дифференцируемая функция и его производная 
также является оригиналом, причем 
при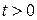 
.
Пусть , 
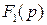. Найдем связь между и 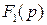. По определению изображения имеем: 
.
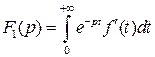Выберем здесь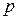 
так, чтобы одновременно выполнялись неравенства
. Выполняя в правой части интегрирование по частям, причем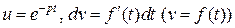 
, находим
.
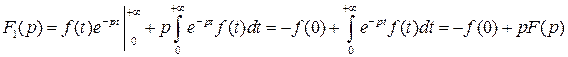Таким образом, из соотношения следует:
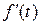
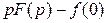(2.2).
Предполагая, что оригинал дифференцируем 
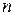раз и что 
также является оригиналом, методом индукции из формулы (2.2) получим следующий результат:
Из соотношения следует соотношение
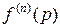
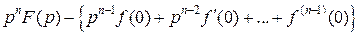. (2.3)
Пример. Изображение функции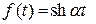 
можно получить следующим образом: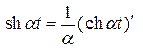 
;
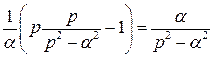Интегрирование оригинала
Примем без доказательства, что если может служить оригиналом, то оригиналом некоторого изображения будет и функция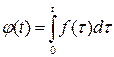 
.
Найдем теперь изображение .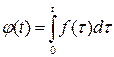
Так как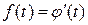 
, то полагая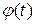 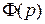, по формуле (2.2) находим связь между 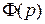и :
,
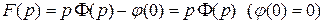откуда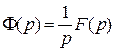 
. Таким образом, из соотношения следует
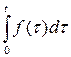
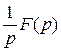. (2.4)
Примеры. 1.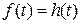 
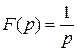, следовательно −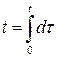 
.
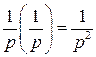По индукции легко получить: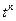 
2. 
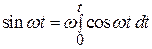
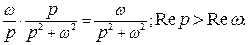
Дифференцирование изображения
В теории функций комплексного переменного доказывается, что несобственный интеграл
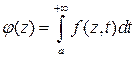, в котором 
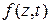есть регулярная функция комплексного переменного 
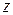в замкнутой области 
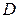и непрерывная функция вещественного переменного 
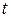при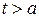 
, можно дифференцировать под знаком интеграла: 
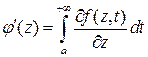, если интеграл этот сходится равномерно относительно .При этом теорема остается верной и для несобственного интеграла, в котором подынтегральная функция становится неограниченной.
Говоря о свойствах изображения, было установлено, что изображение является регулярной функцией комплексного переменного в полуплоскости 
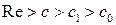и что в этой полуплоскости дифференцирование изображения можно выполнять под знаком интеграла Лапласа. Поэтому из равенства 
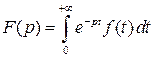следует, что
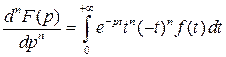. в правой части равенства стоит изображение функции 
. Таким образом, из соотношения следует, что
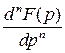(2.5)
Примеры. 1.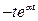 
.
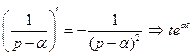
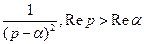2. 
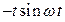
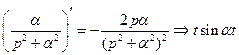
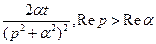
Интегрирование изображения
Пусть функция 
является изображаемой по Лапласу, т.е. имеет место соотношение:
.
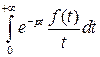Заменим функцию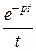 
интегралом 
: 
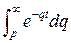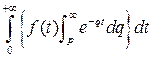
и изменим в правой части порядок интегрирования:
,
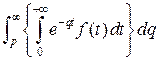
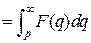где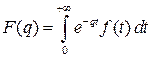 
.
Таким образом, если и функция изображаема по Лапласу, то
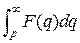
. (2.6)
Пример. 
.
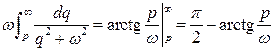