Из определения предыдущего параграфа непосредственно следует, что интеграл от аналитической функции по замкнутому контуру, содержащему внутри себя единственную особую точку выражается через вычет в этой точке: 
. Эта формула легко обобщается следующей теоремой.
Теорема (Основная теорема теории вычетов). Пусть функция f (z) является аналитической всюду в ограниченной замкнутой области G с границей Г за исключением конечного числа изолированных особых точек zk (k = 1,2,…, n), лежащих внутри области. Тогда
Доказательство. Выделим каждую особую точку zk замкнутым контуром γk, лежащим в области G и содержащим внутри себя эту точку (рис.4).
Функция f (z) является аналитической в области, ограниченной контурами Г и γ1,…, γn. По следствию теорем п. 2.2 верна формула 
Отсюда и из предыдущего параграфа следует утверждение теоремы.
Данная формула часто используется для вычисления интегралов от комплексных функций.
Пример. Вычислить интеграл 
где С − окружность 
Решение. Функция имеет два полюса первого порядка, лежащие внутри окружности С. Оба вычета легко определяются (п.2.10). Итак: 
.
2.11 Вычет функции в бесконечно удаленной особой точке.
Определение. Вычетом аналитической функции f (z) в точке z = ∞ называется значение интеграла 
, где С – произвольный замкнутый контур, вне которого f (z) – аналитическая и не имеет особых точек, отличных от ∞. Фактически, контур С − является границей окрестности бесконечно удаленной точки, при обходе которой область остается слева. В силу определения коэффициентов ряда Лорана
получаем: 
Пример. Вычислить Res 
.
Решение. 
.
Из полученных формул следует утверждение:
Теорема. Пусть функция f (z) регулярна на расширенной комплексной плоскости, за исключением конечного числа изолированных особых точек z 1,…, zn −1, zn = ∞. Тогда
Доказательство. Пусть контур С содержит внутри себя все конечные особые точки. В силу
теоремы из п.2.11 и последней полученной формулы имеем: 
. Из второй части равенства следует утверждение теоремы.
Пример. Рассмотрим последний пример: Res[ f,0] = 
= − Res[ f,∞],
т.е. сумма всех вычетов расширенной комплексной плоскости равна нулю.
Выведенная формула может быть записана следующим образом:
.
В такой форме она применяется как при вычислении вычета в бесконечно удаленной точке,
так и справа налево при вычислении интегралов в том случае, когда внутри контура С находится несколько полюсов высокого порядка, а вычет в бесконечно удаленной точке может быть найден достаточно просто непосредственно.
Замечание. Из последней формулы следует, что вычет функции, имеющей в бесконечно удаленной точке устранимую особенность, может быть отличным от нуля.
Вопросы для самопроверки.
1. При каком условии 
не зависит от пути интегрирования?
2. Применима ли формула Коши для вычисления интеграла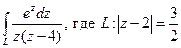 
.
3. Какова связь между нулями и полюсами функции?
4. Чему равна сумма вычетов функции во всех конечных особых точках?
3. Операционное исчисление.
В этом разделе рассматривается одно из основных приложений ТФКП - решение дифференциальных уравнений (как обыкновенных, так и с частными производными).
3.1. Интеграл Фурье
Напомним основные результаты разложения функций в тригонометрические ряды Фурье.
Пусть в промежутке 
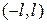функция 
удовлетворяет условиям Дирихле, а именно:
а) ограничена на этом отрезке;
б) кусочно-непрерывна на нем (имеет конечное число точек разрыва первого рода);
в) кусочно-монотонная (в частности, имеет лишь конечное число экстремумов).
Из теории тригонометрических рядов следует, что ряд
(3.1)
представляет собой периодическую функцию с периодом 2 l и сходится к функции f (t) на интервале 
. По теореме Дирихле:
1) в точках непрерывности сумма ряда равна значению функции: 
;
2) в точках разрыва t 1 сумма ряда 
(включая концы интервала, если 
).
Коэффициенты ряда (1.1) определяются по формулам Эйлера-Фурье:
(3.2)
Мы будем рассматривать полученный ряд Фурье только на интервале 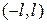. В этом случае формулу (3.1) можно написать в виде: 
(3,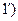 
Легко видеть, что коэффициенты 
и 
удовлетворяют условиям: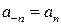 
, 
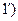. Поэтому формула (3, может быть записана в виде 
или, с учетом формул (3.2),
,
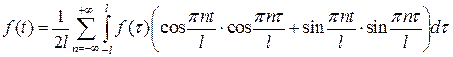откуда 
Если ввести обозначения:
,
то последняя формула будет иметь вид: 
. (3.3)
Пусть функция абсолютно интегрируема на промежутке 
, т.е.
(
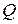− конечное число),
Можно доказать, что при 
равенство (3.3) перейдёт в равенство:
, или 
. (3.4)
Интеграл, стоящий в правой части равенства (3.4), называется интегралом Фурье.
Замечая, далее, что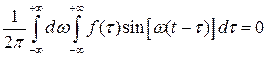 
Пользуясь нечетностью функции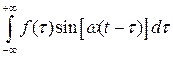 
по аргументу 
, преобразуем формулу (3.4): 
, откуда
. (3.5)
Последний интеграл называется интегралом Фурье в комплексной форме.
