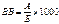Статистичним групуванням називають розчленування, розподіл одиниць сукупності на класи, групи та підгрупи за суттєвими ознаками. Та ознака, що покладена в основу групування, тобто за якою утворюються групи, має назву групувальної.
У системі статистичних методів дослідження метод групувань займає дуже важливе місце. По-перше, він дозволяє дослідити склад та розподіл одиниць сукупності за певною ознакою. По-друге, на його основі базується використання інших статистичних методів (середніх величин, дисперсійний аналіз тощо).
При використанні методу групувань необхідно дотримуватись трьох основних вимог:
- всебічний логічний та економічний аналіз досліджуваних процесів та явищ;
- визначення суттєвих ознак;
- обгрунтоване визначення числа груп та інтервалів групування.
З допомогою групувань вирішують три типи завдань:
а) виділення соціально-економічних типів явищ та процесів; б) вивчення складу та структури сукупності, структурних зрушень та закономірностей розподілу; в) виявлення взаємозв`язку між явищами або показниками, що їх характеризують.
Кожному з названих завдань відповідає окремий вид групування: типологічне, структурне та аналітичне. Крім цього, групування класифікуються за видом групувальної ознаки, а також у залежності від їх числа та співвідношення.
За видом групувальної ознаки групування поділяються на:
1) групування за атрибутивною ознакою; 2)групування за дискретною кількісною ознакою; 3)групування за інтервальною кількісною ознакою; 4)групування за альтернативною ознакою.
За числом групувальних ознак та співвідношенням між ними групування бувають:
а) прості (групувальна ознака одна); б) багатомірні (ознак дві та більше, їх вагомість однакова); в) комбінаційні (ознак дві та більше, вони розглядаються у комбінації); г) ієрархічні (ознак дві та більше, вони мають стале співвідношення “старшості”). Наприклад, групування підприємств за галузями економіки, а кожної галузі – на підгалузі та окремі виробництва.
Використання того чи іншого виду групування обумовлюється метою дослідження, наявністю первинної інформації, можливістю використання комп'ютерної техніки тощо.
13. Основні методологічні питання групування.
До основних методологічних питань групування належать:
- вибір групувальної ознаки;
- визначення числа груп;
- встановлення інтервалів групування.
Визначення групувальної ознаки (або ознак) здійснюється з врахуванням суті та законів розвитку явищ та процесів, що досліджуються. Головна вимога до групувальної ознаки – її суттєвість, тобто вагомість з точки зору мети дослідження. Особливі складності при виборі групувальних ознак виникають при топологічних групуваннях, які передбачають якісні відмінності між групами.
Визначення числа груп у багатьох випадках залежить від особливостей групувальної ознаки. В тому випадку, коли групування здійснюється за атрибутивною ознакою, число груп відповідає числу варіантів цієї ознаки (наприклад, групування населення за рівнем освіти нараховує 7 груп). Якщо групувальна ознака є альтернативною, то завжди утворюється тільки дві групи.
В тому випадку, коли групувальна ознака є кількісною дискретною з обмеженою кількістю варіантів, число груп співпадає з числом варіантів цієї ознаки. У разі групування за інтервальною ознакою кількість груп визначається шляхом логічного аналізу або шляхом випробувань. При цьому виникає потреба утворення інтервалів групування.
Інтервал групування.
Інтервал групування – це проміжок між двома значеннями групувальної ознаки, в межах яких всі одиниці сукупності відносяться до даної групи. Відповідно менше та більше число мають назву нижньої та верхньої межі інтервалу групування, а різниця між ними називається величиною інтервалу.
Інтервал групування називають закритим, якщо у ньому є нижня і верхня межа. В тому випадку, коли одне число відсутнє, інтервал є відкритим зверху або знизу. Наприклад, групування робітників за рівнем середньомісячної заробітної плати (у грн.): до 450, 450-500, 500-600, понад 600.
Інтервали називаються рівними, якщо їх величина у всіх групах однакова. У протилежному випадку утворюються нерівні інтервали, котрі в свою чергу бувають зростаючими або спадаючими.
Інтервали, утворені за однією ознакою, але різні за величиною у різних сукупностях, мають назву спеціалізованих. Наприклад, групування міських поселень та сільських населених пунктів за чисельністю жителів.
Якщо виконується групування з рівними інтервалами, величина інтервалу визначається за формулою:
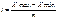,де: Xmax та Xmin – відповідно найбільше та найменше значення групувальної ознаки;
m – число груп.
Орієнтовно число груп можна визначити за формулою Стерджесса:
.
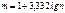Наведену формулу доцільно застосовувати для багаточисельних сукупностей з нормальним розподілом одиниць за групувальною ознакою. В деяких випадках необхідно забезпечити приблизно рівну кількість одиниць у кожній групі, але тоді групування може не мати рівні інтервали.
15. Вторинні групування.
Вторинним групуванням називають групування, які виконуються не по первинних даних, а по вже згрупованих раніше, тобто по рядах розподілу. Вони здійснюються двома способами:
- збільшенням або зменшенням інтервалів групування;
- перегрупування за чисельністю або питомою вагою груп.
Розглянемо на прикладі перший спосіб вторинного групування. Маємо вихідний ряд розподілу лікарень за числом ліжок:
ККількість ліжок Число лікарень
20 – 30 2
31 – 40 7
41 – 50 4
51 – 60 10
61 – 70 5
71 – 80 20
81 – 90 30
91 – 100 60
Разом 138
Необхідно утворити три групи лікарень з
відповідним числом ліжок:
Кількість ліжок Число лікарень
До 50 2 + 7 + 4 = 13
50 – 80 10 + 5 + 20 = 35
понад 80 30 + 60 = 90
Разом 138
Розглянемо другий спосіб вторинного групування, використовуючи наведений ряд розподілу лікарень. Необхідно утворити три групи, які нараховують по 46 лікарень у кожній, тобто по 33,3%.
У першу групу мають увійти перші п'ять груп (2+7+4+10+5=28), а також частина шостої групи (46-28=18). Звідси верхня межа першого інтервалу дорівнює:
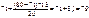
Таким чином, перший інтервал вторинного групування має вигляд:
До 79 включно 46 лікарень (33,3%)
Тоді у другий інтервал входять 2 лікарні з шостої групи, 30 лікарень сьомої групи і частина лікарень з восьмої групи (2+30+14=46). Верхня межа другого інтервалу буде дорівнювати:
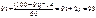
Звідси, другий інтервал має вигляд:
80-93 46 лікарень (33,3%)
Третій інтервал отримуємо автоматично
94-100 46 (60-14) лікарень (33,3%)
Отже, маємо нове групування:
| К-т ліжок | Ч-ло лік | Пит.ваг. |
| До 79 | 33,3 | |
| 80-93 | 33,3 | |
| 94-100 | 33,3 | |
| Разом |
Таким чином, за допомогою вторинних групувань можна здійснювати перетворення груп, одержаних внаслідок первинного групування.
16. Статистичні таблиці.
Статистичні таблиці призначені для найбільш раціонального, наочного та систематизованого викладення результатів зведення та групування. У статистичній таблиці розрізняють підмет та присудок. Підметом таблиці є бічні заголовки (заголовки рядків), як правило, це перелік об`єктів або територій, які характеризуються числовими даними. Присудок таблиці – верхні заголовки (заголовки стовпців або граф), тобто це показники, що характеризують статистичну сукупність. Перетин рядків та граф утворюють клітини таблиці, призначені для числових характеристик.
Таблиця обов`язково повинна мати загальний заголовок, який характеризує зміст таблиці, час та територію, до яких відносяться дані.
Правила побудови статистичної таблиці:
1) таблиця повинна мати оптимальний розмір і стосуватися тільки досліджуваного явища або процесу; 2)загальний та внутрішні заголовки повинні бути чіткі, короткі та змістовні; 3)якщо рядків або стовпців (граф) багато, їх прийнято нумерувати; 4)одиниці виміру показників обов`язково вказуються, у разі потреби для них виділяється графа або рядок; 5)кількісні показники в межах однієї графи або рядка повинні наводитися з однаковою точністю, наприклад, до 0,1 тощо; 6)якщо немає відомостей про розмір явища, у відповідній клітині проставляються крапки (...), відсутність або нульове значення позначають тире (-), якщо клітина не заповнюється проставляється знак “х”, коли число значно менше від інших, записується 0,000.
В залежності від способу побудови підмету статистичної таблиці вони поділяються на прості, групові та комбінаційні. У простій таблиці підмет містить перелік певних об`єктів або періодів часу (дат), країн тощо. Групові таблиці характеризуються тим, що у підметі розташовані групи одиниць або інтервали групування. У комбінаційних таблицях групи за однією ознакою поділяються на підгрупи за іншою.
Розробка присудку таблиці буває простою та комбінованою. У першому випадку наводиться простий перелік показників, а в другому показники беруться у певній комбінації, тоді над декількома графами виконується загальний заголовок.
Після побудови статистичної таблиці виконується її логічний та арифметичний контроль, а також оцінюється якість виконання таблиці. Читання та аналіз статистичних таблиць має велике пізнавальне та практичне значення при аналізі суспільних явищ та процесів.
17. 18. Поняття про види розподілу. Види рядів розподілу.
В результаті статичного групування одержують ряди цифрових показників, які характеризують розподіл одиниць досліджуваної сукупності за варіюючою ознакою. Такі ряди мають назву рядів розподілу.
Ряд розподілу складається з двох елементів – варіант і частот. Варіанти (х) – це окремі значення групувальної ознаки, які розташовані у певній послідовності. Частоти (f) – це числа, які показують, скільки разів певне значення ознаки зустрічається у сукупності, або скільки одиниць припадає на кожну групу.
Ряди розподілу відіграють важливу роль при вивченні складу та структури сукупності, закономірностей розподілу одиниць за досліджуваною ознакою, а також використовуються при визначення середніх величин, показників варіації та взаємозв`язку тощо.
В залежності від характеру групувальної ознаки ряди розподілу поділяються на атрибутивні та варіаційні (кількісні). В атрибутивних рядах розподілу варіанти не мають чисельного виразу, тобто групувальна ознака є якісною (атрибутивною). Наприклад, розподіл респондентів по відношенню до економічної політики уряду:
| РРівні підтримки | Число респондентів, чол. |
| Підтримують | |
| Нейтральні | |
| Не підтримують | |
| Разом |
Варіаційні ряди, варіанти яких мають чисельний вираз, поділяються на дискретні та інтервальні. У першому випадку варіанти являють собою дискретні числа, а у другому – інтервали групування, які у свою чергу можуть бути закритими або відкритими, рівними і нерівними, а останні – зростаючими або спадаючими.
Прикладом дискретного ряду розподілу є розподіл сімей по числу членів сім`ї (по Україні станом на 1.01.2005р.):
Всі сім`ї 14057509
з них сім`ї, що складаються з:
2 чоловік 4939347
3 чоловік 3803941
4 чоловік 3383806
5 чоловік 1209494
6 чоловік 486192
7 чоловік 149295
8 і більше чоловік 85434
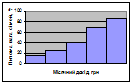
Прикладом інтервального ряду розподілу є розподіл 258 опитаних сімей за розміром місячного доходу на одну особу:
| Місячний дохід сім`ї на одну особу, грн. | Число сімей |
| До 200 | |
| 200 – 400 | |
| 400 – 600 | |
| 600 – 1000 | |
| 1000 і більше | |
| Разом |
Інтервальний ряд розподілу можна перетворити у дискретний, замінивши кожний інтервал його серединою. Середина інтервалу знаходиться як півсума нижньої та верхньої межі. Наприклад, середина інтервалу 200 – 400 грн. становить 300 грн. (200+400/2 =300).
У тому випадку, якщо виконується групування за двома ознаками одночасно, одержують комбінаційний ряд розподілу. Наприклад, розподіл народжених по Україні за віком матері та місцем народження:
| Разом | Міс.пос | Сіл.міс | |
| Всього народж. | |||
| в тому числі в матерів у віці, років: молодше 20 | |||
| 20 - 24 | |||
| 25 - 29 | |||
| 30 - 34 | |||
| 35 - 39 | |||
| 40 - 44 | |||
| 45 - 49 |
 |
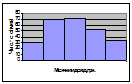Отже, можна побачити, що переважна більшість дітей, як у міських поселеннях, так і у сільській місцевості, народжується у жінок у віці 20 – 29 років.
19. 20. Правила побудови рядів розподілу. Види частот. Щільність розподілу.
При побудові атрибутивних рядів розподілу варіанти розташовують у логічній послідовності, або в порядку спадання чи зростання частот. При використанні дискретних та інтервальних варіаційних рядів важливим є чітке розмежування варіант, для чого використовують різні прийоми. Наприклад, розподіл студентів за ростом:
| 160 – 164 | 160,0 – 164,9 | До 165 см |
| 165 – 169 | 165,0 – 169,9 | 165 - 170 |
| 170 – 174 | 170,0 – 174,9 | 170 - 175 |
| ... | ... | ... |
Середина інтервалу у кожному випадку дорівнює:
 |
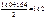
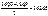
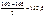
Розрізняють ряди розподілу з абсолютними, відносними та нагромадженими частотами. В першому випадку частота показує абсолютну кількість одиниць у кожній групі, в другому – частку або питому вагу кожної групи у загальній чисельності сукупності. Наприклад, розподіл студентів за віком:
| Вік, років | Ч-ло ст. | Частка | Пит. вага |
| 18-20 | 0,30 | ||
| 20-22 | 0,34 | ||
| 22-24 | 0,26 | ||
| 24-26 | 0,06 | ||
| 26 і більше | 0,04 | ||
| Разом | 1,00 |
Ряди розподілу з абсолютними частотами показують склад сукупності, а з відносними – її структуру. Ряди розподілу з нагромадженими (кумулятивними) частотами характеризують число або питому вагу одиниць, що мають значення ознаки менше певного рівня. Нагромаджені частоти бувають абсолютними та відносними, визначаються вони шляхом сумування (нагромадження) значень відповідних абсолютних та відносних частот по групах. Наприклад, ряд розподілу студентів за віком з нагромадженими частотами в абсолютному та відносному виразі:
| Вік | Число ст. | Нагромадж.час | |||||
| Чол | % | ||||||
| 18-20 | |||||||
| 20-22 | |||||||
| 22-24 | |||||||
| 24-26 | |||||||
| 26 і < | |||||||
Таким чином, 320 студентів або 64% є молодшими 22 років, а 450 студентів або 90% мають вік менше 24 років, 96% студентів молодше 26 років.
Щільність розподілу – це кількість одиниць сукупності, що припадає на одиницю величини інтервалу. Визначається вона за формулою:
fd = f / і,
де f – частота; і – величина інтервалу.
Звідси: f = fd * i. Розрізняють абсолютну та відносну щільність розподілу. Наприклад, розподіл сімей за рівнем місячного доходу:
Отже, найбільшу щільність розподілу має третя група сімей з рівнем місячного доходу 400 – 600 грн.
21. Інтерполяція в рядах розподілу.
Інтерполяція в рядах розподілу використовується в двох випадках. По-перше, якщо необхідно визначити, скільки одиниць (або %) мають значення ознаки менше певного заданого рівня. По-друге, якщо треба знайти значення ознаки, менше або більше якого мають величину показника певна задана кількість або процент одиниць. Для виконання інтерполяції як вихідні дані використовують нагромаджені частоти у абсолютному та відносному виразі та величину інтервалу. Наприклад, маємо ряд розподілу сімей за рівнем місячного доходу на одного члена сім'ї:
| Місячний дохід, | Нагромаджені частоти | ||
| Од. | % | ||
| До 200 | 13,2 | ||
| 200-400 | 33,4 | ||
| 400-600 | 61,3 | ||
| 600-1000 | 88,4 | ||
| 1000 і б | 100,0 | ||
Визначимо, скільки сімей або процентів сімей мають місячний дохід до 500 грн.? Для полегшення розрахунків використаємо графічну інтерпретацію:
400 500 600
86? 158
Отже,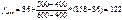 
сім’ї
Або
400 500 600
 |
33,4? 61,3
Отже,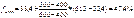 
Таким чином, місячний дохід менше 500 грн. мають 122 сім`ї або 47,4% опитаних сімей.
З допомогою інтерполяції можна відповісти на запитання такого типу: менше якого рівня мають місячний дохід 50% або 129 сімей.
22. Графічне зображення рядів розподілу.
Для графічного подання рядів розподілу використовують три види графіків: гістограму, полігон та кумуляту.
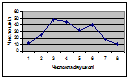
Гістограма будується для інтервальних рядів розподілу. При цьому по осі Хвідкладаються інтервали групування, а по осі У– абсолютні або відносні частоти. В тому випадку, коли виконується групування з рівними інтервалами, ширина стовпчиків однакова, а якщо інтервали групування нерівні - різна. Наведемо приклад побудови гістограми, використовуючи ряд розподілу сімей за рівнем місячного доходу (грн.).
Полігон використовується для графічного зображення дискретних та атрибутивних рядів розподілу. Це лінійний графік, при цьому по осі Х відкладаються значення варіант, а по осі У – частоти. Гістограму можна перетворити у полігон, з`єднавши відрізками прямої середини верхівок стовпчиків. Наведемо приклад побудови полігону, побудованого на основі дискретного ряду розподілу шкіл за кількістю класів:
 |
Кумулята призначена для графічного подання рядів розподілу з нагромадженими частотами. Це може бути стовпчикова діаграма (для дискретного та атрибутивного рядів розподілу – лінійний графік). Будується вона аналогічно попереднім графікам, тільки по осі У подаються нагромаджені частоти. Наведемо приклад побудови кумуляти:
23. Статистичні показники. Їх суть та види.
Статистична інформація, яку одержують у процесі статистичного дослідження, являє собою сукупність статистичних показників.
Статистичний показник — це одна з основний категорій статистики, яка характеризує суспільні явища та процеси у поєднанні кількісної та якісної визначеності.
Будь-який статистичний показник є поєднанням якісної та кількісної складових. Якісна складова показника обумовлюється сутністю та змістом явища і знаходить відображення у назві показника, наприклад, чисельність постійного населення, прибуток від операційної діяльності, ціна тощо. Крім цього, до якісної складової належить одиниця виміру, територія та час, до яких відноситься показник.
Кількісна частина показника — це його чисельне значення у відповідності з якісним змістом. Наприклад, чисельність постійного населення Тернопільської області на 1.01.2002 р. — 1 млн.142 тис.чол.
Статистичні показники повинні мати такі властивості:
· адекватність — спроможність характеризувати ті властивості, що досліджуються; достовірність — відповідність реальному стану речей; точність вимірювання — відповідність змісту показника, організації спостереження та обробки даних діючим вимогам.
Класифікація показників:
1) за способом одержання показники поділяються на первинні та вторинні (похідні). Перші одержують шляхом статистичного спостереження, зведення та групування, а другі розраховуються на основі перших;
2) за ознакою часу показники поділяються на моментні та інтервальні. Моментні показники дають кількісну характеристику явища на певний момент часу, а інтервальні — за період часу (доба, тиждень, декада, місяць, квартал, рік). Наприклад, чисельність студентів на 1.09.2002 р. — моментний показник, а число відрахованих студентів протягом навчального ріку — інтервальний;
3) за можливістю узагальнення (сумування) показники поділяються на адитивні та неадитивні. Значення адитивних показників можна додавати, оскільки їх сума має економічний зміст. Неадитивні показники не можна додавати, оскільки така дія не має економічного змісту.
24. Абсолютні величини, їх види та одиниці виразу.
Абсолютна статистична величина — це характеристика явища, що виражає чисельність сукупності або її частин, а також розміри, обсяги та рівні первинних ознак.
Абсолютні статистичні величини широко використовуються у статистичному обліку та аналізі, управлінні, плануванні, менеджменті, маркетингу тощо. Вони поділяються на індивідуальні, групові та загальні (сумарні). Індивідуальна абсолютна величини відносяться до окремої одиниці сукупності. Групова та загальна відповідно характеризує окрему групу одиниць або всю сукупність разом, їх одержують шляхом сумування індивідуальних величин. Загальна абсолютна величина має назву «обсяг ознаки».
Абсолютні величини — це іменовані числа. Вони виражаються у натуральних, трудових та вартісних вимірниках.
Натуральними або фізичними називають такі одиниці виміру, які відтворюють фізичні властивості одиниць сукупності (вагу, площу, довжину, потужність тощо). Складна одиниця виміру утворюється з допомогою двох простих, наприклад, тоно-кілометр, кВт-год. У разі потреби використовуються умовно-натуральні одиниці виміру. Тоді рівень ознаки обчислюється у одиницях певного еталону. Перехід від натуральних до умовно-натуральних одиниць виміру здійснюється з допомогою перехідних коефіцієнтів.
Наприклад:
| Потужнєдвигуна, кВт | К-ть, шт. | Перех. коео | К-ть в ум-нат.од. |
| 1,0 | |||
| 1,5 | |||
| 2,0 | |||
| Разом | х |
Якщо перший вид двигунів прийнято за еталон, то перехідні коефіцієнти визначаються наступним чином:
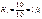
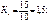
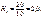
Кількість двигунів в умовно-натуральних одиницях становить:
Н1 = 100 х 1,0 = 100; Н2 = 50 х 1,5 = 75; Н3 = 200 х 2,0 = 400.
Отже, загальна кількість двигунів дорівнює 350 шт., або 575 у.о. в перерахунку на двигуни потужністю 10кВт.
Трудові одиниці виміру (людино-день та людино-година) використовуються для характеристики робочого часу або витрат праці. Вартісні вимірники характеризують розмір явища у грошовому виразі. Вони є найбільш універсальними, але їх головним недоліком є залежність від зміни цін та курсів валют.
25. Відносні величини: економічний зміст та форми виразу.
Відносними величинами називають такі показники, які виражають кількісне співвідношення між ознаками, що характеризують досліджувані явища та процеси.
Відносна величина використовується в тому випадку, коли треба охарактеризувати:
· в скільки разів одна ознака більша або менша за іншу;
· яку частину становить одна ознака відносно іншої;
· скільки одиниць однієї ознаки припадає на 1, 1000, 10000 одиниць іншої ознаки.
Відносну величину завжди одержують шляхом ділення, тому її можна подати у вигляді дробу: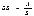 
Показник, що знаходиться у чисельнику (А), називається порівнюваною величиною, а той, що стоїть у знаменнику (Б) — базою порівняння. В залежності від розмірів обох величин використовуються різні форми виразу відносних величин, що дозволяє одержати відносну величину в зручному для сприйняття та інтерпретації вигляді.
У тому випадку, коли А > Б або А@Б, використовується коефіцієнтна форма виразу: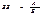 
З формули видно, що результат ділення залишається без змін, при цьому його прийнято визначати з точністю до 0,001. Наприклад, на денній формі навчання є 2500 студентів, а на вечірній — 700.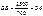 
Отже, на денній формі навчання нараховується у 3,6 рази більше студентів, ніж на вечірній.
Якщо А < Б або А@Б, використовується процента форма виразу (%):
Отже, для одержання цієї форми виразу результат ділення збільшується у 100 разів. Наприклад, у вересні реалізовано продукції на 12500 грн., а у серпні на 17400 грн.
.
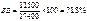Таким чином, у вересні обсяг реалізації продукції становив 71,8% порівняно із серпнем.
У тому випадку, коли А значно менше Б, застосовують промільну форму виразу (‰ — проміле):
