Внутрішньогрупова дисперсія знаходиться окремо для кожної групи, тому для одержання її значення по сукупності в цілому підраховують середню величину:
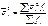 |
38. Правило додавання дисперсій.
Доведено, що загальна дисперсія результативної ознаки дорівнює сумі міжгрупової дисперсії та середньої з внутрішньогрупових дисперсій:
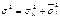 |
Це правило має назву правила додавання дисперсій. Воно використовується для того, щоб розкласти загальну варіацію результативної ознаки на систематичну та випадкову. При цьому мірою систематичної варіації є міжгрупова дисперсія (σм2), а випадкової — середня із внутрішньогрупових дисперсій (σі2).
39. Характеристики форм розподілу. Криві розподілу.
При вивченні форми розподілу в залежності від значень частот розрізняють одно-, дво- та багатовершинні ряди розподілу. Якісно однорідні сукупності мають одновершинний (одномодальний) розподіл одиниць. Наявність декількох вершин свідчить про неоднорідність сукупності.
Серед одновершинних рядів розподілу розрізняють симетричні та несиметричні, госто- та плосковершинні. У симетричних рядах розподілу середня арифметична, мода і медіана співпадають.

х = μ0 = μе
В асиметричних рядах розподілу вершина зміщена вправо або вліво, а напрямок асиметрії є протилежний до зміщення вершини. Так, при правосторонній асиметрії:
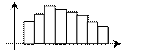 Мо < Ме <
Мо < Ме < 
При лівосторонній асиметрії:
Мо > Ме > 
Напрямок та міру асиметрії характеризують коефіцієнти асиметрії, які обчислюються за формулами:
При правосторонній асиметрії А > 0, при лівосторонній А < 0, при симетричному розподілі А = 0. Вважається, що при |A| < 0,25 асиметрія слабка, при 0,25<|A| <0,5 – середня, при |A| > 0,5 - сильна.
Наприклад, якщо σ = 24,6; X = 180,5; Мо = 164,4; Ме = 170,1 коефіцієнти асиметрії становлять:
Одержані результати свідчать про наявність сильної правосторонньої асиметрії.
Коефіцієнт асиметрії можна також визначити за формулою:
При дослідженні ступеня концентрації одиниць навколо середнього рівня визначають коефіцієнт ексцесу:
При гостровершинному розподілі Е > 0, при плосковершинному Е < 0, а при нормальному розподілі Е = 0.
Закономірність розподілу одиниць сукупності за значеннями варіючої ознаки можна описати певною функцією, яка має назву теоретичної кривої розподілу. Найбільш часто використовується нормальна крива розподілу, а сам розподіл, котрий можна описати цією кривою, має назву нормального розподілу. Він має наступні властивості:
40. Види взаємозв’язків між явищами та процесами.
Одним із найважливіших завдань статистичного аналізу є вивчення та кількісна оцінка взаємозв’язків між соціально-економічними явищами та процесами. Статистичні закономірності взаємозв’язків між ознаками є причинно-наслідковими. Для виникнення певного наслідку необхідні причини та умови, які називають факторами. Ознака, яка характеризує наслідок дії фактора або факторів, має назву результативної. Відповідно, ознака, яка характеризує причину або умову називається факторною.
Усі багато чисельні взаємозв’язки між ознаками, котрі характеризують соціально-економічні явища і процеси, можна поділити на дві групи: функціональні (детерміновані) і стохастичні (ймовірносні або кореляційні) зв’язки.
Функціональні (детерміновані) зв’язки характеризуються тим, що одному значенню факторної ознаки (Х) відповідає одне строго визначене (детерміноване) значення результативної ознаки (Y). Ці зв’язки завжди є повними, тобто значення результативної ознаки на 100% залежить від факторної. Наприклад, тарифний денний заробіток (Y) при фіксованій годинній тарифній ставці залежить від кількості відпрацьованих годин (Х).
100%
Х => Y
При стохастичному (кореляційному) зв’язку одному значенню факторної ознаки (Х) може відповідати декілька значень результативної ознаки (Y). Важливою особливістю цих зв’язків є те, що вони мають риси статистичної закономірності та проявляються у масі спостережень, при достатньо великій чисельності сукупності. Названі зв’язки є неповними, тому що завжди існують невраховані фактори, отже значення Y залежить від значень Х менше, ніж на 100%.
< 100%
Y1  Х Y2
Х Y2
Y3
За напрямком зміни факторної та результативної ознак зв’язки поділяються на прямі та обернені. При прямому зв’язку обидва показники змінюються в одному напрямку, тобто при збільшенні Х зростає також й Y. При оберненому зв’язку напрямок зміни показників протилежний, тобто при зростанні Х зменшується Y.
За аналітичним виразом зв’язки поділяються на лінійні та нелінійні. В залежності від числа факторних ознак розрізняють одно факторні (парні) та багатофакторні (множинні) зв’язки. Для різних-видів взаємозв’язків використовуються відповідні методи їх статистичного дослідження та оцінки.
41. Балансовий та графічний методи.
Балансовий метод вивчення взаємозв’язків застосовується для системи показників, між якими існує балансовий зв’язок, який можна подати наступною формулою:
А+Б=В+Г (1)
Найчастіше у єдину систему пов’язують абсолютні показники, які характеризують наявність та рух різноманітних ресурсів (матеріальних, трудових, фінансових, інформаційних тощо). Наприклад, формула матеріального балансу має вигляд:
| Залишок на початок періоду (А) | + | Надходження за звітний період (Б) | = | Витрати за звітний період (В) | + | Залишок на кінець періоду (Г) | (2) |
Як правило, баланси оформлюються у вигляді таблиць, що складаються в приходної та видаткової частин. Вихідну формулу балансу можна використовувати для розрахунку одного показника, який вважається результативним, через інші, які є факторними. Наприклад:
А=В+Г-Б; Б=В+Г-А; В=А+Б-Г; Г=А+Б-В (3)
В наведеній формулі (3) результативний показник залежить від трьох факторних, а зв’язок є функціональним.
Графічний метод передбачає зображення взаємозв’язку між двома ознаками у вигляді лінії або сукупності крапок. Цей метод дає наочне уявлення про характер взаємозв’язку і найчастіше використовується на початку дослідженні для формування певної гіпотези.
При побудові графіка взаємозв’язку по осі абсцис показують значення факторної ознаки (Х), а по осі ординат – результативної ознаки (Y). Якщо значень Х та Y небагато, будується лінійний графік (Рис.1). В тому випадку, коли таких значень велика кількість, використовується графік кореляційного поля (Рис.2).
На основі одержаного графічного зображення можна зробити наступні висновки: а) про наявність зв’язку між ознаками; б) про його напрямок; в) про аналітичну форму зв’язку; г) про тісноту (щільність, силу) зв’язку.
Основним недоліком даного методу є суб’єктивність висновків, які ґрунтується не на кількісних оцінках, а не візуальному сприйнятті графічного зображення.
42. Метод порівняння паралельних рядів даних.
Для вивчення стохастичних (кореляційних) зв'язків використовується метод порівняння паралельних рядів двох показників, один з яких є факторним (Х), а другий – результативним (Y). При цьому основним завданням застосування цього методу є оцінка тісноти (сили) взаємозв'язку та визначення його напрямку на основі розрахунку спеціальних коефіцієнтів.
Найпростішим показником є коефіцієнт Фехнера (Кф), який розраховується за формулою:

де С – число співпадінь знаків відхилень від середньої;
Н – число наспівпадінь знаків відхилень від середньої.
Якщо виконується нерівність 

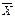 або
або 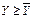 , значенню присвоюється знак ” +”, в протилежному випадку – знак ”-”. В тому випадку, коли по обох показниках знаки однакові, має місце їх співпадіння, а коли вони різні – неспівпадіння. Коефіцієнт Фехнера знаходиться в межах від -1 до +1. Якщо
, значенню присвоюється знак ” +”, в протилежному випадку – знак ”-”. В тому випадку, коли по обох показниках знаки однакові, має місце їх співпадіння, а коли вони різні – неспівпадіння. Коефіцієнт Фехнера знаходиться в межах від -1 до +1. Якщо 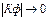 , зв'язок між показниками слабкий, а при
, зв'язок між показниками слабкий, а при 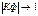 - зв'язок тісний. Цей коефіцієнт має додатне значення при наявності прямого зв'язку, а від'ємне – при оберненому.
- зв'язок тісний. Цей коефіцієнт має додатне значення при наявності прямого зв'язку, а від'ємне – при оберненому.
Більш досконалим показником вважається коефіцієнт кореляції рангів Спірмена  , яких визначається наступним чином:
, яких визначається наступним чином:

де d = rx-ry – різниця рангів факторного та результативного показників.
При цьому під рангом розуміють порядковий номер значення показника у порядку зростання або зменшення. Коефіцієнт кореляції рангів також змінюється від -1 до +1. При 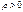 зв'язок між показниками прямий, а при
зв'язок між показниками прямий, а при  - обернений. Якщо
- обернений. Якщо 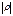 наближається до 1, між показниками існує тісний (сильний) зв'язок, якщо
наближається до 1, між показниками існує тісний (сильний) зв'язок, якщо  <0,3 вважається, що взаємозв'язок практично відсутній.
<0,3 вважається, що взаємозв'язок практично відсутній.
Таким чином, наведені коефіцієнти дають можливість не тальки оцінити тісноту взаємозв'язку між факторною та результативною ознаками, але й визначити його напрямок (прямий чи обернений).
43. Метод аналітичного групування.
Метод аналітичного групування полягає у тому, що сукупність розбивається на групи за факторною ознакою (Х), далі по кожній групі та по сукупності визначаються середні значення Х та Y. Порівняння середній значень факторної та результативної ознак дозволяє зробити певні висновки про наявність та напрямок взаємозв'язку між ними. Крім цього можна визначити показники співвідношення між приростами середніх за формулою: 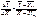 , (6)
, (6)
де 
 - середні значення факторної та результативної ознаки по групах (групові середні).
- середні значення факторної та результативної ознаки по групах (групові середні).
Якщо наведене співвідношення по групах приблизно стале, між показниками існую взаємозв'язок.
Для оцінки тісноти взаємозв'язку між ознаками визначається емпіричне кореляційне відношення  :
:
 , (7)
, (7)
де  - між групова дисперсія результативної ознаки;
- між групова дисперсія результативної ознаки;
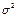 - загальна дисперсія результативної ознаки;
- загальна дисперсія результативної ознаки;
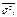 - середня із внутрішньо групових дисперсій результативної ознаки.
- середня із внутрішньо групових дисперсій результативної ознаки.
Емпіричне кореляційне відношення змінюється в межах від 0 до 1. Чим ближче його значення наближається до 1, тим сильнішим є взаємозв'язок між ознаками. При 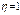 зв'язок вважається функціональним. Крім цього, визначається коефіцієнт детермінації (D), який показує, на скільки відсотків варіація Y зумовлена варіацією Х:
зв'язок вважається функціональним. Крім цього, визначається коефіцієнт детермінації (D), який показує, на скільки відсотків варіація Y зумовлена варіацією Х:
D = 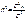 . (8)
. (8)
Крім оцінки тісноти взаємозв'язку необхідно встановити, чи не є відмінність між середніми значеннями Y по групах випадковою (несуттєвою), тобто здійснити перевірку суттєвості зв'язку. Для цього значення  порівнюються з певним критичним значенням, яке знаходиться з спеціальної таблиці, і якщо це відношення більше 1, коливання середніх можна вважати невипадковим, а зв'язок - суттєвим.
порівнюються з певним критичним значенням, яке знаходиться з спеціальної таблиці, і якщо це відношення більше 1, коливання середніх можна вважати невипадковим, а зв'язок - суттєвим.
Для перевірки суттєвості взаємозв'язку між Х та Y часто використовують запропонований Р.Фішером показник, який має назву F-критерія та визначається за формулою:
 , (9)
, (9)
де К2 = n-m, K1 = m-1 - число ступеней волі при кількості одиниць n та кількості груп m.
Критичні значення F-критерія для рівнів значимості 0,05 та 0,01 занесені у спеціальні таблиці. Із цих таблиць у відповідності зі значеннями К1 та К2 визначається так зване табличне значення F-критерія (Fтабл). Якщо виконується умова F>Fтабл, зв'язок між показниками можна вважати суттєвим, (невипадковим).
44. Парний кореляційно-регресійний аналіз.
Стохастичні зв'язки, котрі характеризуються взаємодією середніх значень факторної та результативної ознак, називаються кореляційно-регресійними. Такі зв'язки досліджуються з допомогою кореляційно-регресійного аналізу.
Найважливішою характеристикою кореляційного зв'язку є ліній регресії, тобто функція, котра пов'язує середні значення Х та Y. Кореляційно-регресійна модель взаємозв'язку являє собою рівняння регресії, яке у загальному вигляді записується наступним чином:
 , (10)
, (10)
де ух – теоретичні значення Y;
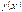 - лінія регресії;
- лінія регресії;
 - залишкова компонента.
- залишкова компонента.
У парному кореляційно-регресійному аналізі переважно використовуються наступні функції (рівняння регресії):
лінійна 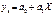
параболічна 
кубічна 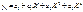
степенева 
гіперболічна  .
.
Розглянемо методику кореляційно-регресійного аналізу на прикладі лінійного зв'язку, який описується лінійним рівнянням регресії. На першому етапі доцільно застосувати графічний метод для формування гіпотези про наявність саме лінійного взаємозв'язку між ознаками.
На другому етапі визначаються параметри лінійного рівняння регресії:
 .
.
Для цього використовується метод найменших квадратів та розв'язується система рівнянь відносно а0 і а1 : 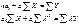

З наведеної системи параметри рівняння регресії розраховуються різними способами, в тому числі за формулами:

Параметри а0 і а1 мають певний економічний зміст, зокрема, а1 називається коефіцієнтом регресії, що показує, на скільки одиниць змінюється Y при збільшенні Х на одну одиницю. Якщо цей коефіцієнт додатний – зв'язок прямий, а якщо від'ємний – зв'язок між показниками обернений.
На третьому етапі за одержаним рівнянням регресії розраховуються теоретичні значення результативної ознаки Yх та показники рівня апроксимації (наближення), які показують розбіжність між фактичними і теоретичними значеннями Y:
- середня квадратична (стандартна) помилка:
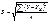 (11)
(11)
- коефіцієнт апроксимації:
 . (12)
. (12)
Чим меншими є значення S та V, тим краще рівняння регресії описує (апроксимує) взаємозв'язок між Х та Y.
На четвертому етапі оцінюється тіснота зв'язку за допомогою лінійного коефіцієнта кореляції(r): 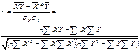 . (13)
. (13)
Значення коефіцієнта кореляції r знаходиться в межах від -1 до +1. При r>0 зв'язок між показниками прямий, а при r<0 – обернений. Якщо: 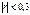 вважається, що зв'язок між Х та Y практично відсутній;
вважається, що зв'язок між Х та Y практично відсутній;  - зв'язок слабкий;
- зв'язок слабкий; 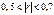 - зв'язок середній;
- зв'язок середній;  - зв'язок сильний;
- зв'язок сильний; 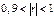 - зв'язок дуже сильний.
- зв'язок дуже сильний.
Коефіцієнт детермінації D=r2 показує, на скільки відсотків варіація Y обумовлюється варіацією Х.
Часто також визначається коефіцієнт еластичності (Е) за формулою:
Е= 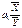 . (14)
. (14)
Цей коефіцієнт показує, на скільки процентів змінюється Y при збільшенні Х на 1%.
На п'ятому етапі здійснюється перевірка суттєвості (невипадковості) взаємозв'язку між показниками за допомогою F-критерія Фішера:
F=  , (15)
, (15)
де К1=m-1; K2=n-m; n – кількість одиниць у сукупності; m - кількість параметрів у рівнянні регресії.
45. Множинна регресія і кореляція.
Як відомо, більшість соціально-економічних показників формується під впливом не одного, а багатьох факторів. Метод побудови моделі такого зв'язку має назву багатофакторного кореляційно-регресійного аналізу. В цьому випадку результативна ознака (Y) пов'язується з допомогою рівняння множинної регресії з двома або більше факторними ознаками (Х1, Х2, Х3,..., Хm).
Найважливішими умовами побудови багатофакторної моделі зв'язку є достатня кількість одиниць у сукупності (як мінімум у 8 разів більше, ніж число факторів) та відсутність мультиколінеарності факторів (близького до функціонального зв'язку між ними). В тому випадку, якщо два факторних показники мультиколінеарні, один з них повинен бути виключений з моделі.
На практиці використовуються два види рівнянь множинної регресії:
- лінійне (адитивне):
 (16)
(16)
- нелінійне (мультиплікативне):
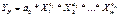
((17)
де а0, а1, а2,..., аm – параметри рівняння множинної регресії;
Х1, Х2,Х3,..., Хm - факторні ознаки.
Оцінка параметрів рівняння множинної регресії здійснюється методом найменших квадратів. Параметри а1, а2 ,..., аm називаються коефіцієнтами регресії та показують, на скільки одиниць змінюється у при збільшенні х на одиницю, при умові, що інші фактори є сталими. Наприклад, рівняння залежності ціни (Y) від рівня продуктивності праці (X1) та якості сировини (X 2):
Ух = 10,2+12,6х1+0,7 х2.
Для вимірювання тісноти взаємозв'язку між двома ознаками, що включені у модель, визначають парні коефіцієнти кореляції (ryx1, ryx2, rx1x2). Тісноту зв'язку між результативною ознакою (Y) та факторною (при спільному впливі всіх факторів) характеризують часткові коефіцієнти кореляції (Ryx1, Ryx2).
Тісноту взаємозв'язку між результативною ознакою та сукупністю всіх факторних ознак визначають на основі коефіцієнта множинної кореляції R. Величина D = R2 називається коефіцієнтом детермінації, що показує, на скільки процентів варіація Y обумовлюється варіацією всіх факторних ознак, включених у модель.
46. Оцінка тісноти взаємозвязку між атрибутивними ознаками.
Для аналізу взаємозв'язку між атрибутивними ознаками будуються спеціальні таблиці, що мають назву таблиць співзалежності. В тому випадку, коли утворюються по дві групи за факторною та результативною ознаками, або коли вони є альтернативними, для оцінки тісноти зв'язку визначають коефіцієнти асоціації та контингенції за формулами:
 і
і 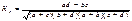 .
.
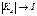 - сильний зв'язок;
- сильний зв'язок;
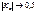 - сильний зв'язок.
- сильний зв'язок.
Для розрахунку названих коефіцієнтів використовують так звані тетрахорічні таблиці, що показують розподіл одиниць за факторною та результативною ознаками.
| Факторна ознака (х) Результативна ознака (у) | х1 | х2 | Разом |
| у1 | 12 а | 198 b | 210 (a+b) |
| у2 | 78 с | 122 d | 200 (c+d) |
| Разом | 90 (а+с) | 320 (b+d) | 410 (n) |
В тому випадку, коли утворюється більше, ніж дві групи по X та Y, тісноту зв'язку оцінюють з допомогою коефіцієнтів співзалежності:
- Чупрова (при m1 = m2):
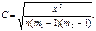
- Крамера (при m1 ≠ m2):
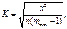 де mmin – менше з двох значень.
де mmin – менше з двох значень.
Значення х2 визначається за формулою:
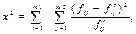
47. Суть вибіркового спостереження.
Вибіркове спостереження є найбільш поширеним видом несуцільного спостереження. При цьому обстеженню підлягає не вся статистична сукупність, а лише її певна частина, яка відбирається за відповідними правилами та представляє сукупність в цілому.
Вибіркове спостереження має суттєві переваги порівняно з суцільним: воно є більш оперативним, вимагає менше коштів та часу на підготовку та проведення. Результати вибіркового спостереження часто є точнішими, оскільки зменшуються помилки реєстрації.
До вибіркового спостереження вдаються тоді, коли проведення суцільного спостереження недоцільне або неможливе.
В процесі вибіркового спостереження вирішуються наступні завдання:
- визначається мета спостереження;
- складається план і програма спостереження;
- визначається вид та спосіб відбору, чисельність вибірки;
- проведення відбору, тобто формування вибіркової сукупності;
- реєстрація ознак;
- розраховуються вибіркові характеристики
- визначаються помилки репрезентативності та поширюються результати на генеральну сукупність.
48. Характеристика генеральної та вибіркової сукупностей.
Вся сукупність одиниць, з яких виконується відбір для подальшого обстеження, називається генеральною сукупністю, а її чисельність позначається N. Частина генеральної сукупності, що попала у вибірку має назву вибіркової сукупності (її чисельність позначається n). Відношення n/N називається часткою відбору, а 100  n/N – процентом відбору.
n/N – процентом відбору.
Як вибіркова, так і генеральна сукупності характеризуються рядом показників, що відповідно називаються вибірковими та генеральними характеристиками. Розбіжність між ними, яка об`єктивно виникає внаслідок несуцільності спостереження, має назву помилки репрезентативності. Помилки репрезентативності, на відміну від помилок реєстрації, можна оцінити (тобто визначити їх розмір), що дозволяє врахувати їх при поширенні результатів вибіркового спостереження на генеральну сукупність.
Генеральні характеристики:
N – чисельність генеральної сукупності;
 – середнє значення ознаки у генеральній сукупності (генеральна середня);
– середнє значення ознаки у генеральній сукупності (генеральна середня);
 2 – дисперсія;
2 – дисперсія;
p – генеральна частка;
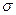 2p – дисперсія альтернативної ознаки
2p – дисперсія альтернативної ознаки 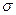 2р = р(1- р).
2р = р(1- р).
Вибіркові характеристики:
n – чисельність вибіркової сукупності; 
х – середнє значення ознаки у вибірковій сукупності (вибіркова середня);
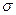 2 – дисперсія;
2 – дисперсія;
W – вибіркова частка;
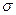 2w – дисперсія альтернативної ознаки
2w – дисперсія альтернативної ознаки 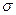 2w = W (1-W).
2w = W (1-W).
Доведено, що для достатньо великих сукупностей генеральна та вибіркова дисперсії співпадають, тому на практиці для розрахунків помилок репрезентативності використовують вибіркову дисперсію.
49. Види та способи відбору.
В залежності від того, скільки разів відібрані для обстеження одиниці приймають участь у відборі, розрізняють повторний та безповторний відбір. При повторному відборі обстежені одиниці ” повертаються” у генеральну сукупність і знову приймають участь у відборі. При без повторному відборі одиниці, що попали у вибірку, більше не приймають участі у відборі, таким чином кожна одиниця може бути відібраною лише один раз






