Групування. Його суть, завдання та види. 4 страница

При формуванні вибіркової сукупності використовують також наступні види відбору:

- індивідуальний, при якому у вибіркову сукупність вибирають по одній одиниці з генеральної сукупності;

^- груповий або серійний, при якому вибирається група (серія) одиниць;

^- комбінований, тобто сполучення перших двох видів відбору.

Розрізняють чотири основних способи формування вибіркової сукупності:

1). власне випадковий відбір (повторний чи безповторний), при якому вибіркова сукупність формується виключно випадково (методом жеребкування, за таблицями чисел тощо);

2). механічний (систематичний) відбір, при якому у вибіркову сукупність попадають одиниці з певними порядковими номерами. При цьому всі одиниці генеральної сукупності спочатку впорядковуються та їм присвоюються порядкові номери. Далі визначається пропорція відбору та крок. Наприклад, пропорція відбору 1/20, отже крок (різниця між порядковими номерами) становить 20. Далі з першої групи випадковим чином визначається перший порядковий номер, а наступні – шляхом додавання кроку відбору. Наприклад, з перших 20 одиниць обрано 7-му, тоді наступні одиниці – 27, 47, 67 і т.д. Цей спосіб відбору є безповторним.

3).типовий відбір передбачає, що генеральна сукупність поділяється на однорідні групи і з кожної групи випадковим або механічним способом формується вибіркова сукупність. Якщо з кожної групи відбирається однаковий процент одиниць, типовий відбір називається пропорційним, а якщо однакова кількість одиниць – непропорційним. Типовий відбір може бути повторним і безповторним.

4). серійний відбір, при якому у вибіркову сукупність відбираються групи одиниць (серії), які надалі обстежуються суцільно.

У статистичній практиці застосовується відбір у часі, наприклад, моментне спостереження, що передбачає реєстрацію ознак на певний момент часу, як правило, через рівні інтервали.

 

50. Помилки вибіркового спостереження: зміст та методика розрахунку.

Помилки вибіркового спостереження виникають внаслідок обстеження частини сукупності, або при порушенні правил формування вибіркової сукупності. Вони проявляються у розбіжності між генеральними і вибірковими характеристиками. Ці помилки поділяються на випадкові та систематичні. Випадкові помилки (помилки репрезентативності) можна оцінити із заданим рівнем імовірності. Систематичні помилки, що виникають внаслідок невдалого відбору, оцінюванню не підлягають, тому їх не можна враховувати.

Випадкові помилки вибіркового спостереження залежать від двох факторів:

- чисельність вибіркової сукупності (або частки чи процента відбору);

- варіації ознаки.

Доведено, що чим більшою є чисельність вибіркової сукупності (частка відбору), тим меншою є помилка вибіркового спостереження, і навпаки, чим більшою є варіація ознаки, Тим більша й помилка.

Залежність величини помилки вибіркового спостереження від названих факторів виражається через формули граничної помилки вибірки:

а) при повторному випадковому відборі гранична помилка визначається

- для середньої = t

- для частки = t

 

б) при без повторному випадковому та механічному відборі гранична помилка визначається за формулами:

-для середньої ;

-для частки .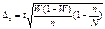

 

51. Визначення обсягу вибірки та способи поширення результатів вибіркового спостереження.

При підготовці вибіркового спостереження виникає необхідність визначити мінімальну чисельність одиниць у вибірці, яка забезпечує її репрезентативність. При цьому величини та W визначаються наближено, або беруться результати попередніх чи пробних досліджень.

Мінімальна чисельність вибіркової сукупності розраховується за формулами:

- при повторному випадковому відборі:

n = 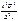та n = ;

- при без повторному випадковому відборі та механічному відборі:

n = та n = .

В статистичній практиці результати вибіркового спостереження найчастіше використовуються для одержання генеральної середньої та генеральної частки.

Якщо вибіркові характеристики мають дискретний характер, то генеральні набувають інтервального вигляду з певним рівнем ймовірності.

Межі генеральної середньої:

x -

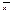
Межі генеральної частки:

w -

В деяких випадках для визначення генеральних характеристик використовується метод прямого перерахунку. При цьому визначається коефіцієнт поправки, який призначений для коректування результатів вибіркового спостереження. Цей метод найчастіше застосовується тоді, коли вибіркове спостереження має на меті перевірку якості суцільного спостереження.

Таким чином, даний метод дозволяє одержати генеральні характеристики у вигляді дискретних величин, на відміну від наведеного раніше.

 

52. Поняття про ряди динаміки.

Ряди статистичних величин, які характеризують зміну явищ у часі, мають назву рядів динаміки. Вони складаються з двох елементів – показника часу (t) та рівнів ряду динаміки (у). Рівні ряду динаміки – це числові значення показника, котрі розташовані у хронологічній послідовності та відносяться до відповідного моменту або періоду часу.

Ряди динаміки мають велике значення для дослідження закономірностей зміни соціально-економічного розвитку у часі (закономірностей динаміки), для прогнозування та статистичного моделювання.

Найважливішою умовою побудови рядів динаміки є співставність усіх рівнів. Неспівставність може виникнути з багатьох причин: територіальні та адміністративні зміни, перегляд методики розрахунку показників, їх одиниць виміру, зміна цін тощо. Для приведення ряду динаміки у співставний вигляд використовують метод прямого перерахунку або метод зімкнення ряду динаміки.

Метод прямого перерахунку полягає у тому, що нові рівні ряду динаміки розраховуються повторно з врахуванням тих змін, які відбулися. Метод зімкнення ряду динаміки передбачає, що нові значення рівнів ряду динаміки визначаються на основі перехідного коефіцієнту. Цей коефіцієнт розраховуються як відношення значення показника в нових умовах до значення того ж показника у старих умовах, які обчислені за однаковий період або момент часу.

 

53. Види рядів динаміки та правила їх побудови.

Ряди динаміки класифікуються за показником часу та способом виразу рівнів ряду. За показником часу розрізняють моментні та інтервальні ряди динаміки. В момент них рядах рівні ряду відносяться до певного моменту часу або дати, а в інтервальних – до періоду або інтервалу. В моментних рядах динаміки сума рівнів ряду не має економічного місту, тому середній рівень ряду визначається за формулою середньої хронологічної: , (1)

де n- кількість рівнів ряду динаміки.

Наприклад, маємо ряд динаміки чисельності працівників:

 

Дата 1.01.97 1.01.98 1.01.99 1.01.00 1.01.01 1.01.02 1.01.03

Чисельність

працівників, чол. 820 834 811 807 800 804 740

Середня чисельність працівників за 1997-2003 рр. Становить:

В інтервальних рядах динаміки сума рівнів ряду характеризує значення показника за більший інтервал часу і є самостійним показником. Середній рівень ряду в даному випадку визначається за формулою середньої арифметичної простої або зваженої:

(2) Наприклад, маємо ряд динаміки виробництва продукції протягом року:

Квартал І ІІ ІІІ ІУ

Обсяг виробництва, т 200 212 195 220

Середньоквартальне виробництво продукції становить: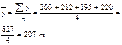

Отже, за квартал обсяг виробництва продукції становить в середньому 207 тонн.

За способом виразу рівнів розрізняють ряди динаміки абсолютних, відносних та середніх величин.

 

54. Аналітичні показники динаміки.

Для вивчення закономірностей динаміки використовується система показників, які характеризують напрямок та інтенсивність зміни у часі досліджуваної ознаки.

Абсолютний розмір змін у часі показує абсолютний приріст. Ланцюговий абсолютний приріст () характеризує зміну показника за одиницю часу в абсолютному виразі:

. (3)

Базисний абсолютний приріст () показує зростання або зменшення показника в абсолютному виразі порівняно з рівнем, прийнятим за базу, тобто за певний період часу:

. (4)

Між наведеними показниками існує взаємозв'язок: сума ланцюгових абсолютних приростів дорівнює базисному абсолютному приросту, а різниця двох послідовних базисних абсолютних приростів дорівнює ланцюговому:

(5)

Середній абсолютний приріст показує середній розмір зміни показника за одиницю часу і розраховується за формулою:

. (6)

Для характеристики відносної зміни показника у часі використовуються коефіцієнти або темпи росту (зростання):

 

а) коефіцієнти росту:

ланцюгові Кл=

базисні Кб=

б) темпи росту:

ланцюгові Тр= х100 базисні Тб= х100.

Середній коефіцієнт або темп росту розраховується як середня геометрична за формулою:

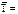
(7) . (8) Між ланцюговими та базисними коефіцієнтами зростання існує взаємозв'язок: добуток ланцюгових коефіцієнтів росту дорівнює базисному коефіцієнту, а відношення двох послідовних базисних коефіцієнтів росту дорівнює ланцюговому:

Тб= 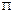Тл; Тл= .

 

Темп приросту характеризує відносну швидкість зміни показника у часі, як правило, у процентному виразі. Темпи приросту визначаються наступним чином:

ланцюгові: Тпр= = Тл-100 (9)

базисні: Тпр= = Тб-100. (10)

Середній темп приросту розраховується за формулою:

.

Абсолютний вміст (значення) 1% приросту характеризує абсолютний розмір одного проценту зміни показника і визначається за формулами:

А= . (11)

 

55. Методи обробки рядів динаміки.

У статистичній практиці не завжди можна обмежитися визначенням аналітичних показників ряду динаміки. Для всебічного аналізу закономірностей динаміки необхідно використовувати різноманітні методи обробки рядів з метою виділення їх загальної тенденції (тренду).

Для порівняння швидкості зміни двох або більше взаємопов’язаних показників використовують метод приведення рядів динаміки до єдиної основи. Суть цього методу полягає у тому, що вихідні ряди динаміки абсолютних значень показників замінюються базисними темпами зростання, котрі визначені відносно однакового моменту (періоду) часу. Порівняння базисних величин дозволяє зробити висновок про те, який з показників зростає або зменшується швидше.

Для виявлення тенденції зміни показника у досить довгих рядах динаміки використовують метод збільшення інтервалів часу. При цьому вихідні рівні ряду замінюють сумарними або середніми значеннями показника за більші періоди часу.

Для обробки ряду динаміки з метою зменшення коливань його рівнів використовується метод рухомої середньої. Суть цього методу полягає у тому, що первинний ряд динаміки замінюється рядом середніх значень, підрахованих на основі рухомих сум. Рухома сума визначається шляхом додавання рівнів ряду, включених в інтервал вирівнювання (переважно це 3, 5, 7 рівнів).

Найбільш ефективним методом виявлення тенденції динаміки є аналітичне вирівнювання. Його суть полягає у тому, що вихідний ряд динаміки описують рівнянням тренду, яке розглядається як аналітичний вираз загальної тенденції зміни у часі (тренду).

На практиці найчастіше використовують наступні рівняння тренду:

лінійне
параболічне
показникове
степеневе
гіперболічне

Розглянемо техніку виконання аналітичного вирівнювання на прикладі лінійного рівняння тренду. Параметри а­­_0­ та а­₁ знаходяться з системи нормальних рівнянь методом найменших квадратів. Для спрощення підрахунків параметр часу t задаються таким чином, щоб . Тоді

Параметр а­₁ показує, на скільки одиниць в середньому змінюється показник за одиницю часу. Вирівняні (розрахункові) значення одержуються шляхом підстановки в одержане рівняння тренду заданих значень t.

Для перевірки адекватності моделі (рівняння тренду) використовують наступні показники:

- середнє квадратичне (стандартне) відхилення. ;

- коефіцієнт апроксимації .

Вважають, що рівняння тренду достатньою мірою апроксимує (описує) ряд динаміки, якщо V<10%. Отже, лінійне рівняння тренду дуже добре описує вихідний ряд динаміки.

56. Інтерполяція та екстраполяція в рядах динаміки.

Інтерполяцією називають метод знаходження невідомого рівня в межах ряду динаміки. При цьому враховують закономірність зміни показника у часі, що сформувалася у певному інтервалі. Інтерполяцію здійснюють на основі двох суміжних з невідомим рівнів ряду динаміки, або з використанням середніх показників динаміки. Загальні формули для визначення невідомого рівня ряду (y_i) мають вигляд:

Екстраполяція — це метод знаходження значення показника за межами відомого ряду динаміки. Цей метод передбачає поширення тенденції ряду у минуле або майбутнє, тому розрізняють ретроспективну та прогнозну екстраполяцію.

Екстраполяція здійснюється на основі середніх показників ряду динаміки або з допомогою рівняння тренду. Прогнозна екстраполяція першим способом виконується за формулами:

де l — період випередження (l = 1, 2, 3...), y_n – останній відомий рівень ряду динаміки.

При використання для прогнозу рівняння тренду в одержане рівняння підставляють наступні значення параметру часу (t + l), наприклад, у лінійне рівняння тренду:

Наведемо приклад розрахунку названих показників, використовуючи раніш знайдене рівняння тренду:

Дні	у		yt	y – y­t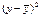
				-2
Сум				х

Розмах варіації:

R = y_max – y_min =326 – 300 = 26 (од.)

Середній рівень ряду:

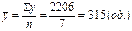
Середнє квадратичне відхилення:

Коефіцієнт варіації:

Рівняння тренду:

.

Стандартне відхилення:

Коефіцієнт апроксимації:

Отже, ряд динаміки має слабку варіацію, а лінійне рівняння тренду добре описує (апроксимує) вихідні дані. Вплив випадкових факторів дуже слабкий, оскільки V_a = 0,6%.

Розрахункові значення у­_t одержують на основі середніх показників або рівняння тренду. Коливання фактичних значень ряду динаміки навколо тренду, що проявляється у відхиленні їх від розрахункових, обумовлюється впливом випадкових факторів і вимірюється абсолютними та відносними показниками:

стандартне відхилення:

коефіцієнт апроксимації:

Показники S та V_a використовують також для підбору оптимального рівняння тренду, для якого .