НЕЭЛЕКТРОЛИТОВ
Свойства раствора всегда отличаются от свойств каждого из его компонентов. Это изменение обусловлено, с одной стороны, взаимодействием между компонентами и, с другой стороны, уменьшением концентрации молекул каждого из веществ при распределении в нем другого вещества. Влияние этих факторов усиливается с ростом концентрации растворяемого вещества, их количественный учет очень сложен.
Общие закономерности, характерные для процесса растворения и растворов, изучают на примере очень разбавленных растворов, при образовании которых тепловой и объемный эффекты пренебрежимо малы, т. е. ∆H ≈ 0 и ∆V ≈ 0. В таких растворах частицы растворенного вещества находятся на большом расстоянии друг от друга и их взаимное влияние очень незначительно, а растворитель практически не меняет своих свойств.
В основе количественного описания свойств реальных растворов лежат закономерности, полученные для идеальных растворов. Разбавленные растворы приближаются к идеальным, свойства таких растворов описываются более простыми уравнениями. Идеальным называется раствор, в котором энергия взаимодействия между молекулами растворенного вещества и молекулами растворителя одинакова. В среде идеального раствора молекулы растворенного вещества распространяются подобно идеальному газу. Идеальный раствор образуется без теплового эффекта (∆Н = 0) и без изменения объема (∆V = 0) смешиваемых компонентов. Движущей силой образования такого раствора является возрастание энтропии (∆S > 0). Понятие об идеальном растворе –воображаемое; реальные растворы могут быть только более или менее близки к идеальным. Так, при смешении жидкостей, молекулы которых неполярны и сходны между собой по структуре и химическим связям, тепловые и объемные изменения очень малы. Например, для процесса образования раствора толуола и бензола ∆H ≈ 0 и ∆V ≈ 0. Если при образовании раствора двух жидкостей происходит лишь хаотическое распределение частиц без межчастичного взаимодействия, то теплота смешения равна нулю, а энтропия меняется лишь в результате изменения концентрации компонентов.
1. Давление пара над растворами.
При рассмотрении разбавленного раствора примем, что растворенное вещество не является электролитом.
В результате естественного процесса испарения над жидкостью образуется пар, давление которого можно измерить с помощью манометра (рис. 7). Эндотермический процесс испарения обратим: одновременно протекает экзотермический процесс конденсации. При определенных условиях устанавливается равновесие (∆G = 0). Равновесное состояние системы жидкость - пар при данной температуре характеризуется давлением насыщенного пара.

Рис. 7. Схема измерения
давления насыщенного пара
Представим себе, что в равновесную систему жидкость - пар введено нелетучее вещество* (его переход в паровую фазу невозможен). При образовании раствора концентрация жидкости - растворителя уменьшается, его мольная доля Х1 становится меньше единицы; это вызывает нарушение равновесия жидкость - пар. В соответствии с принципом Ле Шателье начинает протекать процесс, стремящийся ослабить влияние воздействия, т. е. происходит конденсация пара. Это означает снижение давления пара. Таким образом, можно заключить, что давление пара над раствором p1 меньше, чем над чистым растворителем p1°.
Понижение давления над раствором тем значительнее, чем больше вещества содержится в растворе или чем меньше мольная доля растворителя в растворе, т. е. давление насыщенного пара растворителя над раствором p1 пропорционально мольной доле растворителя X1:
p1 = K X1.
Физический смысл коэффициента пропорциональности К в этом уравнении можно показать путем следующих рассуждений. В пределе, когда X1 = 1, т. е. растворенного вещества нет, p1= p1°, т. е. К = p1°.
Следовательно, это уравнение может быть записано так:
p1 = p1° X1
т. е. давление насыщенного пара растворителя над раствором равно произведению его давления над чистым растворителем на мольную долю растворителя (первый закон Рауля, 1887 г.).
Последнему уравнению можно придать несколько иной вид.
Так как X1 = 1 – X2 (где X2 - мольная доля растворенного вещества), то
p1 = p1°(1 - X2) = p1° - p1° X2 или p1° - p1= p1° X2
Разделив последнее равенство на p1°, получим
(p1° - p1)/ p1° = X2
Следовательно, относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества (другая формулировка первого закона Рауля, строго применимого для идеальных растворов неэлектролитов).
В случае раствора, состоящего из летучих компонентов, парциальное давление пара любого летучего компонента идеального раствора прямо пропорционально его мольной доле
pi = pi° Xi,
где pi° – давление насыщенного чистого компонента; Xi – мольная доля i-го компонента; pi° – парциальное давление пара i-го компонента.
Данное соотношение не зависит ни от природы растворителя, ни от при-роды и концентрации других компонентов. Оно зависит только от его собственной концентрации в растворе. Если раствор состоит из летучих компонентов 1 и 2, то
p1 = p1° X1, p2 = p2° X2. (1')
Общее давление идеального раствора равно сумме парциальных давлений (закон Дальтона):
p = p1+ p2= p1о.X1 + p2° X2
Или, после преобразования,
p = p2о.+ (p1° - p2°)X1
Графическое изображение полученных закономерностей для идеального раствора из летучих компонентов 1 и 2 дано на рис. 8.

Рис. 8. Зависимость давления пара pi от мольных долей Хi для бинарной системы, подчиняющейся закону Рауля.
На длине горизонтального отрезка, условно принимаемого за единицу, откладывается от его левого конца мольная доля компонента 2 X2. В любой точке длины отрезка содержание компонента 1 будет определяться из соотношения X1 = 1 – X2. Концы отрезка символизируют содержание чистых компонентов: справа X1 = 1, слева X2 = 1. p1° и p2° отвечают давлениям паров двух рассматриваемых веществ в чистом состоянии. Диагональные линии показывают изменение парциального давления каждого из компонентов в зависимости от его мольной доли в растворе. правая (тонкая) линия – изменение парциального давления компонента Б в зависимости от его содержания в растворе. Штриховой линией показано общее давление над раствором, создаваемое парами обоих веществ и зависящее от состава.
В природе не существуют идеальные растворы, за исключением растворов изотопов, оптических изомеров; близка к идеальному раствору смесь бензол – толуол.
Но чем ближе компоненты раствора друг к другу по своим физическим свойствам, тем лучше этот раствор подчиняется закону Рауля. Так, растворы жидких органических оптических изомеров и растворы изотопов ведут себя почти в точном соответствии с законом Рауля. Близка к идеальному раствору смесь бензол – толуол. Однако для большинства растворов обнаруживаются отклонения и иногда довольно значительные. Причем, в различных системах наблюдаются как положительные, так и отрицательные отклонения от этого закона. На рис. 9 приведены кривые зависимости давления пара от состава раствора, отражающие поведение реальных растворов с положительным (рис. 9а) и отрицательным (рис. 9б) отклонениями от идеальности. Положительное отклонение от идеальности имеет место тогда, когда энергия между одноименными молекулами (А-А, Б-Б, В-В) больше, чем между различными молекулами (А-Б, А-В...).
В первом случае каждая молекула старается окружить себя подобными молекулами и вытолкнуть из сферы своего влияния чужеродные молекулы, повышая тем самым давление раствора. Растворы с положительным отклонением образуются с трудом, энтальпия образования такого раствора больше нуля. Растворы с отрицательным отклонением от идеальности образуются в тех случаях, когда энергия взаимодействия разнородных молекул больше, чем однородных, их смешение сопровождается выделением тепла (∆H < 0).
 |
а) б)
Рис 9. Кривые давления насыщенного пара компонентов в растворах: а) с положительным отклонением от идеального; б) с отрицательным отклонением от идеального; n – линия Рауля
Из рис. 9 видно, что закон Рауля выполняется на концах кривых, совпа-дающих с пунктирной прямой (линией Рауля – линией идеальности), т.е. в сильно разбавленных растворах (мольная доля растворенного вещества ниже 0.01).
2. Температуры кипения и отвердевания растворов
В прямой зависимости от давления насыщенного пара над раствором нелетучего вещества находится температура кипения раствора.
Если парообразование происходит не только со свободной поверхности жидкости, но и внутри ее, то этот процесс называют кипением. Температурой кипения жидкости является температура, при которой давление ее насыщенного пара равно внешнему давлению (так, при 101 кПа температура кипения воды равна 100°С, бензола 80°С).
Понижение давления пара растворителя в результате растворения в нем вещества означает необходимость повышения температуры кипения раствора для восстановления нарушенного равновесия жидкость - пар. Тогда давление насыщенного пара будет доведено до первоначального, например атмосферного. Таким образом, температура кипения раствора выше температуры кипения растворителя.
Как видно из рис. 10, температура кипения идеального раствора тем выше температуры кипения чистого растворителя, чем больше его концентрация: при mo= 0 < m1 < m2 Tкип, o < Tкип, 1 < Tкип, 2 и, следовательно,
ΔTкип = Tкип, i.- Tкип, o > 0
С понижением давления пара над раствором связана и более низкая температура отвердевания раствора, чем у чистого растворителя (температура отвердевания – это температура, при которой давление пара над жидкостью становится равным давлению пара над твердой фазой) (рис. 10). Температура отвердевания раствора отвечает выделению из него первого кристалла твердой фазы - кристаллического растворителя (выделение в виде кристаллов даже малого количества растворителя приведет к уменьшению мольной доли растворителя в растворе). Здесь используется термин «отвердевание» в смысле «начало замерзания» вместо часто применяемого при рассмотрении этого вопроса термина «замерзание». Замерзание означает полное затвердевание раствора, которое достигается при гораздо более низкой температуре, чем начало замерзания.

Рис. 10. Зависимость давления насыщенного пара растворителя над чистым растворителем (mo) и над растворами (m1 и m2) от температуры
Кристаллы растворителя будут находиться в равновесии с раствором только тогда, когда давления насыщенного пара растворителя над кристаллами и над раствором одинаковы, т. е. когда кривая давления пара над кристаллами (кривая A0B на рис. 10) имеет общую точку с соответствующей кривой испарения (точка A0 для чистого растворителя, точки A1 и A2 для растворов с концентрацией m1 и m2 соответственно). Как видно из рис. 10, температура отвердевания раствора ниже температуры отвердевания чистого растворителя.
Так как для разбавленных растворов понижение давления пара растворителя пропорционально концентрации, то и повышение температуры кипения и понижение температуры отвердевания разбавленных растворов пропорциональны концентрации растворенного вещества. В выражении данной зависимости концентрацию принято указывать через моляльность m (моль/1 кг растворителя):
ΔTкип = E·m
ΔTзам = К·m
Коэффициенты пропорциональности Е и К называются соответственно эбулиоскопической и криоскопической постоянной. Математически E = ∆Ткип и K = ∆Tотв при m = 1 моль/кг, однако при моляльности m = 1 раствор столь далек от большого разбавления (в одномоляльном растворе 342 г тростникового сахара приходится на 1 л воды!), что приведенные соотношения становятся несправедливыми. Чтобы найти численные значения Е и К, результаты измерения температуры кипения и начала замерзания очень разбавленных растворов следует экстраполировать на концентрацию растворенного вещества, равную 1 моль/кг Н2O. Таким образом, Е и К являются экстраполяционными постоянными.
Постоянные Е и К не зависят от природы растворенного вещества, а характеризуют лишь растворитель. Можно показать, что
Е = RT2исп /1000 λисп; K = RT2пл /1000 λпл,
где где Tкипи Tпл– соответственно температуры кипения и плавления чистого растворителя λиспи λпл– удельные теплоты испарения и кипения растворителя. Значения постоянных Е и К для некоторых растворителей приведены в табл. 5.
Таблица 5.
Эбулиоскопические (Е) и криоскопические (К) постоянные
некоторых растворителей
| Растворитель | E | K | Растворитель | E | K |
| Вода | 0,516 | 1,86 | Уксусная кислота | 3,1 | 3,9 |
| Бензол | 2,57 | 5,12 | Нитробензол | 5,27 | 6,9 |
| Тетрахлорметан | 5.30 | 29.80 |
Поскольку ∆Ткип и ∆Тотв изменяются пропорционально числу молей растворенного вещества, а каждый моль содержит одинаковое число молекул (6,022·1023), то эти характеристики раствора зависят только от числа частиц растворенного вещества. Отсюда следует, что повышение температуры кипения и понижение температуры отвердевания раствора пропорциональны числу частиц растворенного вещества и не зависят от его природы (второй закон Рауля).
Следствие из второго закона Рауля: эквимоляльные растворы различных неэлектролитов кипят и замерзают при одной и той же температуре.
3. Осмотическое давление
Представим себе, что в сосуд (рис. 11) с чистым растворителем опущен цилиндр с раствором. Нижняя половина цилиндра изготовлена из материала, проницаемого для растворителя, но не пропускающего частицы растворенного вещества (полупроницаемая перегородка)*. В цилиндре перемещается поршень. Таким образом, имеется неравновесная система: мольная доля растворителя в сосуде Х = 1, в растворе Х < 1. Поэтому в системе начнется самопроизвольный процесс выравнивания концентраций. Молекулы растворителя из объема с их большей концентрацией (из чистой растворителя) будут диффундировать через проницаемую только для них перегородку в раствор, где их концентрация меньше (обратный переход растворенного вещества исключен).
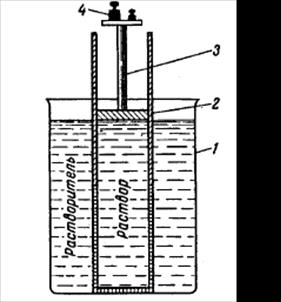
Рис. 11. Схема опыта,
поясняющего осмотическое
давление:
1 – сосуд с растворителем;
2 – сосуд с раствором;
3 – поршень;
4 – груз
Гидростатическое избыточное давление, создаваемое раствором, препятствующее диффузии растворителя через полупроницаемую перегородку в раствор, называется осмотическим давлением.
В 1887 г. Пфеффером экспериментально были найдены две закономерности, которым подчиняется осмотическое давление растворов неэлектролитов:
а) в разбавленных растворах неэлектролитов при данной температуре осмотическое давление прямо пропорционально концентрации С (моль/л).
б) при одной и той же концентрации осмотическое давление разбав-ленного раствора неэлектролита прямо пропорционально абсолютной температуре
Я.Г. Вант-Гофф обратил внимание на аналогию между законами Пфеффера и газовыми законами Гей-Люссака и Бойля-Мариотта, описывающими состояние идеального газа. Анализируя числовые данные, полученные при измерениях осмотического давления Пфеффером, он показал, что величина осмотического давления для разбавленных растворов неэлектролитов может быть выражена уравнением:
πоcм = СRT или πоcмV = nRT,
причем коэффициент пропорциональности оказался универсальной константой, численно равной газовой постоянной R (во второй формуле концентрация С выражена числом молей n растворенного вещества в единице объема V).
Формулировка закона Вант-Гоффа: Осмотическое давление разбавленного раствора неэлектролита равно тому давлению, которое оказывало бы растворенное вещество, если бы оно, находясь в газообразном состоянии при той же температуре, занимало тот же объем, который занимает раствор.
Осмос лежит в основе многих явлений, протекающих в природе.
На практике широко используется понятие изотонических растворов. Изотоническими называются растворы с одинаковым осмотическим давлением.
Осмотическое давление на границе “раствор – полупроницаемая перегородка – растворитель” весьма важно в жизнедеятельности организмов и растений. Оно лежит в основе регулирования водного баланса клеток. В медицине им руководствуются при приготовлении изотонических растворов с кровью (физиологический раствор), с раствором желудочного сока и тому подобное.
В технике используют обратный осмос, происходящий при приложении к раствору давления, превышающего осмотическое. Тогда через полупроницаемую перегородку «выдавливается» чистый растворитель. Обратный осмос применяется для очистки сточных вод и опреснения морской воды.
Закономерность, установленная Вант-Гоффом, так же как и законы Рауля, используется для определения относительной молекулярной массы, так как она численно равна мольной массе, входящей в эти уравнения.
На практике наиболее часто используют криоскопический метод определения молекулярных масс. Он особенно удобен для изучения органических соединений. Исследуемое вещество обычно растворяют в бензоле и с помощью точного термометра (термометр Бекмана) определяют ∆Tотв. Реже применяют эбулиоскопический метод, основанный на измерении ∆Ткип.
Осмотический метод оказался применимым также для определения молекулярных масс растворов высокомолекулярных соединений. Соотношения Рауля для этой цели неприменимы из-за невозможности приготовления разбавленных растворов и трудности, связанной с достижением равновесия. Зависимость осмотического давления растворенного высокомолекулярного вещества от его концентрации описывается соотношением
πоcм = gRT / M + A g2 или πоcм/g = RT / M + A g,
где g – масса полимера (в граммах). Член (A g2) учитывает специфику строения и кинетики полимерных молекул.
Опытным путем находят зависимость величины πоcм/g от массовой концентрации соединения. Экспериментальные данные наносят на график (рис. 12).
Экстраполируя величины πоcм/g к нулевой концентрации, определяют длину отрезка на оси ординат, которая равна величине RT/M, и таким образом определяют молекулярную массу высокомолекулярных соединений.
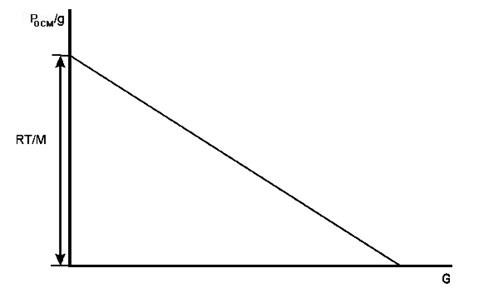
Рис. 12. Графическое представление зависимости πоcм / g = RT / M + A g






