Законы распределения случайных величин. Биномиальный закон распределения

Биномиальный закон распределения.

Этот закон характеризует распределение случайного числа появления события А в n независимых опытах, если вероятность появления события А в каждом опыте постоянная и равна p, а вероятность не появления события А равна g =1-p.

С ,

где m – число появления события А.

В теории вероятностей доказано, что математическое ожидание этой случайной величины равно:
,

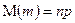а дисперсия числа появления события А равна:

.

Закон Пуассона.

Этот закон характеризует распределение прерывной случайной величины, которая может принимать только целые неотрицательные значения: 0, 1, 2,..., m,..., причем последовательность этих значений теоретически не ограничена. Вероятность того, что эта величина примет определенное значение m, выражается формулой:

,

где a – некоторая положительная величина, называемая параметром закона Пуассона.

В теории вероятностей доказано, что математическое ожидание такой случайной величины равно:

,

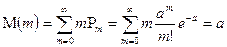а дисперсия также равна a. Это замечательное свойство закона Пуассона позволяет идентифицировать закон распределения для экспериментального ряда чисел как закон Пуассона.