1. Найти производные неявных функций и вычислить их значение при 
:
а)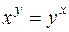 
.
Преобразуем данное выражение к виду:
и, согласно (2), получим:
Вычислим, используя исходное выражение функции, значение 
при :
, логарифмируя это выражение по основанию 
, получим:
, 
, откуда 
. Подставляя значения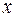 
и в найденное выражение производной, находим:
.
б) 
.
Обозначив левую часть выражения через 
, вычислив частные производные 
и 
и воспользовавшись формулой (2), находим:
.
Вычислим, используя исходное выражение функции, значение при :
,
решая квадратное уравнение, получим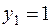 
и 
.
и 
.
2. Найти производные неявных функций:
а) 
.
Обозначив левую часть выражения через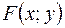 
, вычислив частные производные 
, 
и 
и воспользовавшись формулой (1), находим:
; 
9. Частные производные и дифференциалы высших порядков
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Если функция 
определена в некоторой области D, то ее частные производные 
и 
тоже будут определены в той же области или ее части.
Будем называть эти производные частными производными первого порядка.
Частные производные первого порядка обычно зависят от тех же аргументов, что и сама функция, и каждую из них можно дифференцировать по каждому аргументу.
1°. Частные производные от частных производных первого порядка называют частными производными второго порядка и обозначают:
.
Продолжая дифференцировать полученные равенства, получим частные производные третьего порядка:
;
;
.
Аналогично определяются и обозначаются частные производные четвертого, пятого и более высоких порядков.
2°. Частные производные старших порядков вида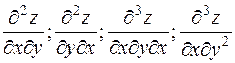 
и т.д. называются смешанными производными.
Теорема. Если функция и ее частные производные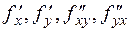 
определены и непрерывны в точке М(х, у) и ее окрестности, то смешанные производные, отличающиеся только последовательностью дифференцирования, равны, т.е. верно соотношение:
.
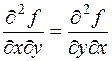Согласно этой теореме, функция двух переменных имеет 3 различных частных производных второго порядка; 4 различных частных производных третьего порядка и, вообще, 
различных частных производных 
-го порядка.
Аналогично определяются дифференциалы высших порядков.
…………………
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего в скобках выражения.
Дифференциал 2-го порядка позволяет вывести приближенную формулу, выражающую функцию через дифференциал:
.
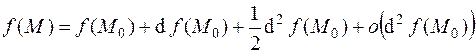Дифференциалы 1-го и 2-го порядка применяют для исследования функции нескольких переменных на экстремум.
