1. Найти производные сложных функций:
а) 
; 
; 
.
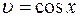Здесь 
- сложная функция одной независимой переменной 
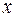. Пользуясь формулой (2), получим:
б) 
; 
; 
.
Здесь - сложная функция двух независимых переменных 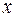и . Пользуясь общими формулами (1), найдем:
в) 
; 
; 
.
Здесь 
- сложная функция одной независимой переменной 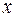. Пользуясь формулой (2) для полной производной, получим:
.
2. Найти 
и 
, если 
; 
; 
.
;
.
8. Дифференцирование неявных функций
1°. Переменная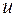 
называется неявной функцией нескольких переменных 
, если она задана уравнением
которое не разрешено относительно .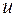
При этом если функция 
и ее частные производные 
, 
, …, 
, 
, определены и непрерывны в некоторой точке 
и вблизи нее, и если 
, а 
, то уравнение вблизи точки 
и в самой этой точке определяет функцию 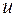как однозначную, непрерывную и дифференцируемую функцию от .
Для вычисления частных производных 
, 
, …, 
нет необходимости выражать 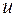в явном виде.
Производные неявной функции 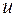, заданной уравнением , при соблюдении указанных выше условий, определяют по формулам:
; 
… 
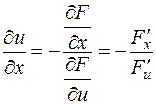(1)
В частности, если - неявная функция одной независимой переменной 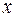, уравнением 
, то ее производная:
(2)
