1.Найти полный дифференциал функции:
а) 
.
Находим частные производные:
; 
.
Умножая частные производные на дифференциалы соответствующих аргументов, получим частные дифференциалы функции:
; 
.
Искомый полный дифференциал находим как сумму частных дифференциалов:
.
б) 
.
;
;
в) 
.
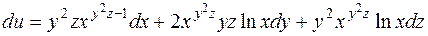
г) 
.
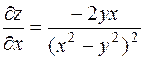
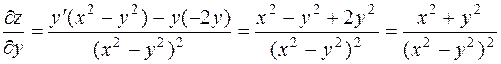
2. Вычислить значение полного дифференциала функции 
при 
; 
; 
; 
; 
. Подставляя числовые значения, получаем 
.
6. Приближенные вычисления с помощью полного дифференциала. Линеаризация функции
Пусть функция 
дифференцируема в точке 
. И пусть значение функции и ее частных производных вычислить в точке проще, чем в точке 
. Найдем полное приращение этой функции от точки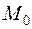 
к точке 
:
. (1)
Выразим из формулы (1) значение функции в точке :
, (2)
где 
; 
и т.д.
Воспользуемся выражением полного приращения функции в виде:
.
Видно, что при достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно со сколь угодно малой относительной погрешностью заменить ее полным дифференциалом:
,
исключая точки, в которых частные производные 
.
Отсюда, возвращаясь к выражению (2), находим, что приближенное значение функции в произвольной точке , отстоящей достаточно близко от точки , можно вычислить по формуле:
Последнее равенство позволяет также линеаризовать функцию, т.е. заменить исходную функцию 
в окрестности точки 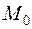линейной функцией.
