1. Вычислить приближенно значение:
а) 
.
Предположим, что - это частное значение функции 
в точке 
и что вспомогательная точка - 
, тогда:
;
, 
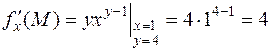
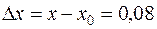Пользуясь формулой приближенных вычислений функции, получаем
.
б) 
Пусть данное выражение есть частное значение функции 
в точке 
. В качестве вспомогательной точки возьмем 
. Тогда
, 
; 
,
Таким образом, 
.
в) 
Пусть данное выражение есть частное значение функции 
при x = 1, y = 2, z = 1.
Из этого выражения определим
, 
; 
Найдем значение функции 
.
Находим частные производные и их значения во вспомогательной точке:
Полный дифференциал функции u равен:
Точное значение этого выражения: 1,049275225687319176.
2. Линеаризовать функцию 
в окрестности точки 
.
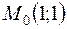Найдем значения функции и ее частных производных в указанной точке:
;
.
Пользуясь формулой линеаризации функции, получаем
.
7. Дифференцирование сложных функций
1°. Переменная 
называется сложной функцией нескольких переменных 
, если она задана через посредство промежуточных аргументов 
:
,
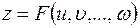где 
, 
,…, 
.
Частная производная сложной функции по одной из независимых переменных равна сумме произведений ее частных производных по промежуточным аргументам на частные производные этих аргументов по независимой переменной:
(1)
………………
Если, в частности, все промежуточные аргументы будут функциями одной независимой переменной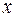 
, то и будет сложной функцией только от 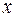. Производная такой сложной функции (от одной независимой переменной) называется полной производной и определяется формулой:
(2)
Формула (2) получается из формулы для полного дифференциала функции 
путем деления на 
.
