1.Вычислить частное значение функции:
а) 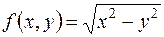 при
при 

б)  в
в 

2.Построить область изменения переменных 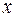 и
и  , заданную неравенствами:
, заданную неравенствами:
а)  ,
,  .
.
Этим неравенствам удовлетворяют координаты каждой точки, находящейся внутри и на границе прямоугольника, стороны которого лежат на прямых 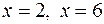 ,
,  . Этот прямоугольник и есть область изменения переменных
. Этот прямоугольник и есть область изменения переменных 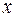 и
и  (рис. а). Такая область, в которую входит и ее граница, называют замкнутой.
(рис. а). Такая область, в которую входит и ее граница, называют замкнутой.
б)  .
.
Данная область – совокупность всех точек, лежащих внутри эллипса  . Область открытая (рис. б).
. Область открытая (рис. б).
в)  .
.
Данная область – круговое кольцо, ограниченное окружностями  и
и  с общим центром в начале координат и радиусами, равными 2 и 3. Область замкнутая (рис. в).
с общим центром в начале координат и радиусами, равными 2 и 3. Область замкнутая (рис. в).
г)  .
.
Открытая область, ограниченная биссектрисой первого координатного угла и осью абсцисс (рис. г).

3.Найти область определения функций:
а)  .
.
 . Геометрическое изображение этой функции (график) – это плоскость, пересекающая координатные оси в точках
. Геометрическое изображение этой функции (график) – это плоскость, пересекающая координатные оси в точках 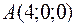 ,
,  и
и  .
.
б) 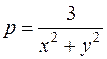 .
.
Из условия, что знаменатель не должен обращаться в нуль:  находим
находим  и
и  одновременно. Отсюда: область определения данной функции – вся числовая плоскость, за исключением точки
одновременно. Отсюда: область определения данной функции – вся числовая плоскость, за исключением точки  .
.
в)  .
.
Из условия, что подкоренное выражение быть неотрицательным:  находим
находим  . Отсюда: область определения данной функции – круг с центром в точке
. Отсюда: область определения данной функции – круг с центром в точке  и радиусом
и радиусом  . (Внутри круга подкоренное выражение положительно, на его границе – равно нулю, а вне круга – отрицательно.)
. (Внутри круга подкоренное выражение положительно, на его границе – равно нулю, а вне круга – отрицательно.)
Графическим изображением данной функции является полусфера, расположенная над плоскостью хОу (рис.2).
 Рис. 2.
Рис. 2.
в)  .
.
Область определения этой функции находим из условия  . Точки, удовлетворяющие этому неравенству, лежат внутри I и III квадрантов.
. Точки, удовлетворяющие этому неравенству, лежат внутри I и III квадрантов.
г)  .
.
Область определения этой функции – вся числовая плоскость, за исключением прямой  .
.
е)  .
.
Область определения этой функции – совокупность значений 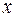 и
и  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  . На плоскости хОу эта область представляет собой полосу, ограниченную параллельными прямыми
. На плоскости хОу эта область представляет собой полосу, ограниченную параллельными прямыми  и
и 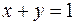 .
.
2. Предел ФНП. Непрерывность
1°. Расстояние между двумя точками в  -пространстве задается равенством
-пространстве задается равенством

2°. Окрестностью точки  радиуса
радиуса  называется совокупность всех точек
называется совокупность всех точек  , которые удовлетворяют условию
, которые удовлетворяют условию
 .
.
3°. Число А называется пределом функции  в точке
в точке 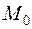 :
:

если абсолютное значение разности  будет меньше любого наперед заданного положительного числа e > 0, когда расстояние
будет меньше любого наперед заданного положительного числа e > 0, когда расстояние  меньше некоторого положительного числа d (зависящего от e).
меньше некоторого положительного числа d (зависящего от e).
Для функции двух переменных записывают: 
4°. Для непрерывности функции  в точке
в точке 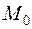 необходимо выполнение следующих условий:
необходимо выполнение следующих условий:
1) функция должна быть определена в точке 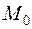 и вблизи нее;
и вблизи нее;
2) функция должна иметь предел, когда точка  стремится к
стремится к 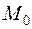 произвольным способом;
произвольным способом;
3) этот предел должен быть равен значению функции в точке 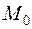 :
:
 (1)
(1)
5°. Функция  , непрерывная в каждой точке некоторой области называется непрерывной в этой области.
, непрерывная в каждой точке некоторой области называется непрерывной в этой области.
6°. Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:
1) Функция  не определена в точке
не определена в точке  .
.
2) Не существует предел  .
.
3) Этот предел существует, но он не равен  .
.
7°. Функция двух переменных  может иметь множество точек разрыва. Если они составляют линию, то она называется линией разрыва функции.
может иметь множество точек разрыва. Если они составляют линию, то она называется линией разрыва функции.
Например, функция  разрывна в каждой точке окружности
разрывна в каждой точке окружности 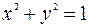 . Эта окружность есть линия разрыва данной функции.
. Эта окружность есть линия разрыва данной функции.




