Якщо вершина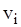 
є кінцем ребра 
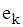то говорять, що вони інцидентні: вершина 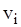інцидентна ребру 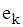і ребро 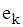інцидентно вершині 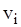. У той час як суміжність являє собою відношення між однорідними об'єктами (вершинами), інцидентність — це відношення між різнорідними об'єктами (вершинами і ребрами).
При розгляді орграфів розрізняють позитивну інцидентність (дуга виходить із вершини) і негативну інцидентність (дуга заходить у вершину).
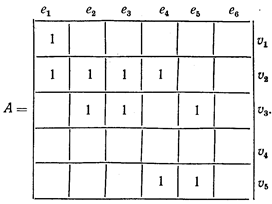
Розглядаючи інцидентність вершин і ребер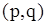 
- графа, можна представити його матрицею інцидентності розміру 
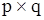, рядки якої відповідають вершинам, а стовбці— ребрам. Для неориєнтованого графа елементи цієї матриці визначаються по наступному правилу: 
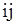-елемент дорівнює 1, якщо вершина 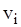інцидентна ребру 
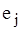, і дорівнює нулю, якщо 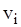і 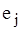не інцидентні. У випадку орграфа ненульовий 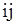-елемент дорівнює 1, якщо 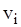початкова вершина дуги 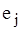, і дорівнює -1, якщо 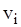— кінцева вершина дуги .
|
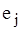Кожен стовпець матриці інцидентності містить обов'язково два одиничних елементи (для орграфа ці елементи завжди мають різні знаки і рівні відповідно 1 і —1). Кількість одиниць у рядку дорівнює ступеню відповідної вершини (для орграфа кількість позитивних одиниць визначає позитивний ступінь, а кількість негативних одиниць — негативний ступінь). Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець — петлі.
Варто мати на увазі, що нульовий стовпець матриці інцидентності лише вказує на наявність петлі, але не містить відомостей про те, із якою вершиною ця петля зв'язана (у практичних додатках це може бути несуттєво).
