Нерідко завдання на графах вимагають виділення різних маршрутів, що володіють визначеними властивостями і характеристиками. Маршрут довжини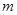 
визначається як послідовність 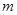ребер графа (не обов'язково різних) таких, що граничні вершини двох сусідніх ребер збігаються. Маршрут проходить і через усі вершини, інцидентні вхідним у нього ребрам. Прикладами маршрутів на графі мал. 3.3, а можуть служити послідовності 
, 
. Перший маршрут проходить через послідовність вершин 
і з'єднує вершини 
і 
, а другий — через послідовність вершин 
і з'єднує вершини і . Замкнутий маршрут приводить у ту ж вершину, із якої він почався.
Маршрут, усі ребра якого різні, називається ланцюгом, а маршрут, для якого різні усі вершини, називається простим ланцюгом. Замкнутий ланцюг називається циклом, а простий ланцюг — простим циклом. Так, на графі мал. 3.3, а 
— ланцюг, 
— простий ланцюг, 
— цикл,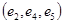 
— простий цикл.
Цикл, що містить усі ребра графа, називається ейлеровим циклом (завдання про кенигсбергскі мости зводиться до з'ясування існування такого циклу), а граф, у якому є такий цикл, називається ейлеровим графом. Простий цикл, що проходить через усі вершини графа, називають гамільтоновим.
Критерій існування ейлерового циклу. Для існування в графі ейлерового циклу необхідно і достатньо щоб ступені усіх вершин були парними.
Для гамільтонових циклів ніякого загального правила не знайдено.
Орієнтовані маршрути на орграфі визначаються аналогічно з тією різницею, що початкова вершина кожної наступної дуги маршруту повинна збігатися з кінцевою вершиною попередньої дуги. Інакше кажучи, рух по маршруту допускається тільки в напрямках, зазначених стрільцями. Маршрут, що не містить повторюваних дуг, називається шляхом, а той, що не містить повторюваних вершин — простим шляхом. Замкнутий шлях називається контуром, а простий замкнутий шлях- простим контуром. Граф (орграф) називається циклічним (контурним), якщо він містить хоча б один цикл (контур), у противному випадку він називається ациклічним (безконтурним). Поняття ланцюга і циклу застосовні і до орієнтованих графів. При цьому напрямки дуг не враховуються, тобто власне кажучи замість орграфа розглядають неориєнований співвіднесений йому граф.
