Зв'язковий граф може бути розділений на незв'язні підграфи видаленням із нього деяких вершин і ребер (при видаленні вершин виключаються і всі інцидентні їм ребра, а при видаленні ребер вершини зберігаються). Якщо існує така вершина, видалення якої перетворює зв'язковий граф (або компоненту незв'язного графа) у незв'язний, то вона називається точкою зчленування (мал. 3.8, а). Ребро з такими ж властивостями називається мостом (мал. 3.8, б). Ясно, що при наявності моста в графі є, принаймні, дві точки зчленування.
Граф називається нероздільним, якщо він зв'язковий і не має
точок зчленування (наприклад, граф на мал. 3.5., а є нероздільним). Граф, що має хоча б одну крапку зчленування, є розділимим і називається сепарабельним. Він розбивається на блоки, кожний із який являє собою максимальний нероздільний підграф (на мал. 3.8, в показані блоки 
графа мал. 3.8, б).
Кожне ребро графа, як і кожна вершина (за винятком крапок зчленування), належать тільки одному з його блоків. Більш того, тільки одному блоку належить і кожний простий цикл. Звідси випливає, що сукупність блоків графа являє собою розбивка безлічей ребер і простих циклів на підмножини, що не перетинаються.
 |
|
Мал. 3.8. Розделимі графи.
а— с крапкою зчленування; б — із мостом; в — блоки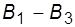 
графа з мостом
У ряді додатків теорії графів блоки можна розглядати як компоненти. Це звичайно припустимо, коли зв'язку блоків за допомогою крапки зчленування несуттєві або коли істотні властивості графа зв'язані тільки з його простими циклами (контурами). У таких випадках можна розглядати незв'язний граф як зв'язковий розделимий граф, що утвориться шляхом такого об'єднання компонент, щоб кожна з них була блоком (це завжди можна зробити, об'єднавши, наприклад, по одній вершині кожного блока в крапку зчленування). Подібні операції використовуються при розгляді графів електричних ланцюгів.
