Дві вершини графа називають зв'язаними, якщо існує маршрут, що з'єднує ці вершини. Граф, будь яка пара вершин якого зв'язана, називають зв'язковим графом. Очевидно, у зв'язковому графі між будь-якими двома вершинами існує простий ланцюг, тому що з маршруту, що їх зв'язує, завжди можна видалити циклічну ділянку, що проходить через деяку вершину більш одного разу (мал. 3.6, де маршрут між вершинами 
і 
зображений жирними лініями).
Якщо граф не зв'язковий, то множину його вершин можна єдиним способом розділити на підмножини, що не перетинаються, кожне з який містить усі зв'язані, між собою вершини і разом із інцидентними їм ребрами утворить зв'язковий підграф. Таким чином, незв'язний граф являє собою сукупність окремих частин (підграфів), називаних компонентами. На мал. 3.7 показаний підграф, що складається з трьох компонент (ізольована вершина вважається компонентою).
Часто відношення зв’язності ускладнюється додатковими умовами. Граф називають циклічно зв'язковим, якщо будь-які дві різні вершини містяться в циклі (наприклад, граф на мал. 3.5, а циклічно зв'язковий, а граф на мал. 3.6 — ні, тому що вершина не міститься ні в якому циклі з іншими вершинами). Граф називають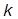 
-зв'язковим, якщо будь-яка пара різних вершин зв'язана, принаймні 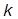ланцюгами, що не мають спільних вершин (крім початкової і кінцевої). Так, граф на мал. 3.5, а двузв’язний, а на мал. 3.6 — однозв’язний.
Видаляємий
цикл
| Простий ланцюг Мал. 3.6. Зв'язковий граф. | Мал. 3.7. Незв'язний граф, що складається із трьох компонент  .
|
Зв’язність орієнтованих графів визначається так само, як і для неориєнтованих (без врахування напрямків дуг). Специфічним для орграфа (або змішаного графа) є поняття сильної зв’язності. Орграф називають сильно зв'язковим, якщо для будь-якої пари його вершин і існує шлях з в і з у (наприклад, граф на мал. 3.2, а сильно зв'язковий). Граф, що представляє план міста з одностороннім рухом по деяких вулицях, повинний бути сильно зв'язковим, тому що в противному випадку знайшлися б вершини (площі і перехрест), між якими не можна було б проїхати по місту без порушення правил руху.
