Нормальное распределение

Нормальный закон распределения характеризуется плотностью вероятности вида

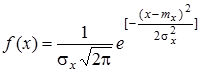, (3.17)

где m_x, σ _x – соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х.

Нормальный закон - это двухпараметрический закон, для его использования нужно знать m_x и σ _x.

Вероятность безотказной работы определяется по формуле

P (t) = 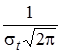, (3.18)

а интенсивность отказов - по формуле

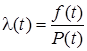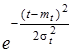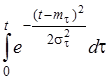= / , (3.18а)

где m_t,σ _t – математическое ожидание и среднее квадратическое отклонение времени жизни объекта.

При нормальном распределении случайная величина может принимать любые значения от -∞ до +∞. Поэтому использовать выражения (2.17), (2.18) можно только для случая m_t / σ_t >=2.5, когда вероятность появления отрицательных значений практически равна 0 (характерно для элементов систем автоматического управления [3.3]).

Если значения математического ожидания и среднего квадратического отклонения времени безотказной работы таковы, что m_t /σ _t < 2.5, ее распределение может быть лишь усечённым нормальным.

Для усеченного на интервале (t ₁, t ₂)распределения нормирующий множитель

(3.19)

условно принимается равным единице, если отношение средней наработки до отказа к среднему квадратическому отклонению наработки до отказа больше 2,5.

Показатели надежности при нормальном распре­делении вычисляется с помощью нормированной функ­ции Лапласа (интеграл Гаусса- Лапласа)

, (3.20)

где u = (t - m_t)/σ _t. Известно, что интеграл Гаусса-Лапласа – нечетная функ­ция [3.1, 3.2, 3.3].

Тогда получим формулы для вычисления:

вероятности отказа

Q (t) = 0,5 + Φ(u),(3.21)

вероятности безотказной работы

P (t) = 0,5 - Φ(u). (3.22)

Можно пользоваться нормальным законом распределения при анализе надежности элементов, подверженных процессам старения или износа.