При решении задач анализа надежности сложных систем, имеющих множество состояний работоспособности, удобно использовать модель случайного процесса, дискретного по состояниям и непрерывного во времени, и определять вероятности нахождения системы в том или ином состоянии [3.4]. В общем случае число таких состояний больше или равно двум (для простой системы).
Обозначим:
S (t) = i – состояние системы в момент времени t равно i (0 
,
n – общее количество возможных состояний системы,
Δ t 
,
Pij (t +Δ t) – условная вероятность перехода системы из состояния S (t) = i в момент времени t в состояние S (t +Δ t) = j (0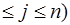 
в момент времени t +Δ t,
λ ij – интенсивности перехода системы из состояния S (t) = i в момент времени t в состояние S (t +Δ t) = j (0 
в момент времени t +Δ t.
Если вероятности перехода Pij (t +Δ t) (0 не зависят от поведения системы до момента времени t, то такой процесс называется марковским.
Если вероятности перехода Pij (t +Δ t) = Pij (Δ t) = λ ij Δ t не зависят от t, то такой процесс называется марковским однородным процессом.
Для такого процесса время пребывания системы в состоянии S (t) = i (0 
подчиняется экспоненциальному распределению (см. п. 3.3.1).
Предполагается, что интенсивности переходов 
удовлетворяют условиям:
,
= 
, (3.24)
где - интенсивность сохранения состояния i (0 
.
Вероятности 
(0 - пребывания системы в i состоянии определяются системой дифференциальных уравнений следующего вида:
- начальные условия, 
(3.25)
.
Система дифференциальных уравнений (3.25) называется уравнениями Колмагорова [3.4].
Будем использовать модель марковских однородных процессов для определения показателей надежности восстанавливаемых и резервированных систем.
