Классическая парадигма теории линейных колебаний – это система из массы и пружины, показанная на рисунке 1.52.
Если отсутствуют возмущающие силы и трение, то система колеблется с частотой, независимой от амплитуды колебаний:
.
Рисунок 1.52 - Классический механический осциллятор с пружиной, массой и демпфером
В таком состоянии энергия попеременно переходит из упругой энергии пружины в кинетическую энергию массы, и наоборот.
Включение затухания делает свободные колебания затухающими, так что амплитуда колебаний массы имеет следующую временную зависимость:
,
где 
.
Говорят, что затухание до критическое, когда 
критическое, когда 
, и сверхкритическое, когда 
.
Одно из классических явлений в линейных колебательных системах – резонанс при гармоническом возбуждении. Дифференциальное уравнение, описывающее систему в этих условиях, имеет вид:
.
Если при постоянной амплитуде 
изменять вынуждающую частоту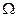 
, то абсолютная величина стационарного смещения массы достигает максимума вблизи естественной частоты 
, а более точно – при 
. Это явление изображено на рисунке. для вынужденного движения линейного осциллятора с затуханием.
Эффект выражен ярче при слабом затухании. В структурированных системах это явление широко распространено, и инженеры хорошо знакомы с проблемой усталостного разрушения конструкций и машин при сильных резонансных колебаниях.
Если линейная механическая система имеет много степеней свободы, ее часто моделируют системой связанных осцилляторов из пружин и масс, обнаруживая при гармоническом возбуждении появление множества резонансных частот. Такое поведение часто наталкивало на предположение, что каждый максимум в спектре колебаний соответствует, по меньшей мере, одной степени свободы.
Рисунок 1.53 - Классические резонансные кривые (зависимость амплитуды отклика от частоты)
В нелинейных колебательных системах это не так. В отличие от своего линейного аналога, нелинейная система с одной степенью свободы может возбудить много частот. В любом случае математическая теория линейных систем хорошо разработана и запрограммирована в мощных пакетах математического обеспечения для компьютеров. Другое дело – нелинейные задачи.
