Идея метода статистического моделирования (метода Монте-Карло) заключается в моделировании возможных реализаций параметров работоспособности системы. При этом, для получения конкретной реализации, случайным образом задаются входные воздействия и с помощью математической модели, описывающей поведение системы, определяются параметры ее функционирования, в частности, значения ее функций работоспособности.
Для определенности рассмотрим случай, когда работоспособность системы определяется выполнением системы неравенств: 
. Тогда надежность системы будет равна 
Очевидно, что выполнение всех условий работоспособности эквивалентно выполнению одного неравенства
, где 
(i = 1,2,…n).
Соответственно выражение для оценки надежности примет вид
,
где 
плотность распределения случайной величины 
.
Для расчета по этой формуле требуется определить выборку значений случайной величины . С этой целью для каждой i-той реализации рассчитываются значения параметров
и выбирается минимальный из них 
. В результате получаем выборку значений 
. Полученная выборка используется для нахождения закона распределения случайной величины . Методы оценки числовых характеристик случайных величин по статистическим данным рассмотрены во второй главе пособия.
Для решения задач методом Монте-Карло требуется большое количество случайных чисел. Эти числа получаются с помощью специальных датчиков, подключенных к компьютеру.
При решении задачи достаточно получить равномерно-распределенные случайные числа. От равномерно-распределенных случайных чисел x можно перейти к любому другому распределению 
. В дальнейшем будем считать, что функция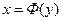 
непрерывна и монотонна (см. рис. 1.24). Тогда для каждого значения 
можно определить соответствующее значение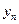 
, удовлетворяющее уравнению 
(см. рис. 1.24).
Рис. 1.24 Схема получения случайных чисел с заданной функцией распределения .
В частности, полагая 
этим способом получим нормально распределенную случайную последовательность 
, соответствующую случайной величине Y с математическим ожиданием 
и дисперсией 
. Линейное преобразование 
дает нормально распределенную случайную последовательность 
, соответствующую случайной величине Z, для которой математическое ожидание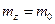 
и дисперсия 
.
