Для нахождения среднего времени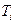 
пребывания системы в i –ом состоянии воспользуемся преобразованием Лапласа для вероятности нахождения системы в этом состоянии
Переходя к пределу при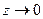 
, получим
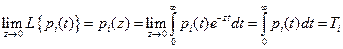
Соответственно для производных получим
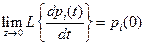, где 
, 
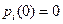(i=2,3,…n)
Учитывая полученные соотношения и применяя предельный переход к обоим частям
алгебраических уравнений (1.41),получим систему уравнений относительно .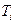
Знание 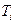позволяет определить среднее время работы системы до достижения любого j-го состояния 
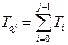. Для схемы «гибели-размножения» величина 
может быть также рассчитана по соотношению
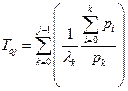
Знание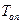 
позволяет найти асинптотическую оценку надежности восстанавливаемых систем
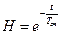, где n- состояние отказа.
Пример 1. Определить среднее время до отказа резервированной системы.
Кратность «горячего» резерва равна трем. Интенсивность отказа элементов равна 
. Элементы системы не восстанавливаются.
Решение:
Для графа системы, представленного на рис. 1.20, система алгебраических уравнений примет вид
.
Рис. 1.20 Граф состояний системы.
После преобразований получим
Пример 2. Определить среднее время до отказа той же системы при условии, что ее элементы восстанавливаются. Интенсивность восстановления равна 
.
Решение:
Для графа системы, представленного на рис. 1.21, система алгебраических уравнений примет вид
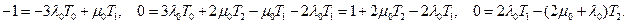
Рис. 1.21 Граф состояний системы.
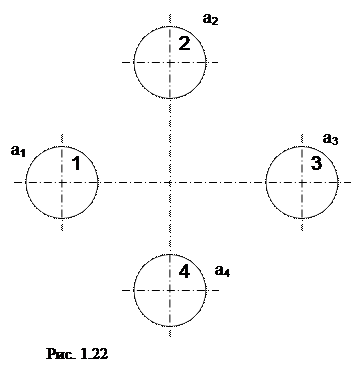
После преобразований получим
.
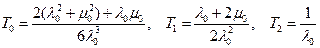1.3.9. Общее резервирование.
В заключении остановимся на оценке надежности при таком резервировании, когда для обеспечения успешного функционирования системы необходимо, чтобы определенное число устройств сохраняло свою работоспособность. Например, для выполнения программы достаточно иметь ДУ, состоящую из l одинаковых двигателей. Для повышения надежности в ДУ включают дополнительно m резервных двигателей.
Для упрощения выкладок анализ общего резервирования проведем для двигательной установки, состоящей из четырех изолированных двигателей, допускающей возможность отказа любых двух из них. Схема двигательной установки представлена на рис. 1.22. Согласно условию, ДУ будет выполнять поставленную задачу при следующих ситуациях:
- ни один из двигателей не отказал (событие А0);
- отказал один из двигателей (событие А1);
- отказали два двигателя (событие А2).
Тогда вероятность безотказной работы ДУ можно представить в виде
Н = Р{ А0 U А1 U А2} (1.62)
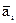В дальнейшем обозначим безотказное функционирование i-го двигателя, как выполнение события аi. Тогда отказ этого двигателя определяется противоположным событием. С учетом введенных обозначений событие Аi можно записать так
А0 = {a1∩a2∩a3∩a4} (1.63)
 |
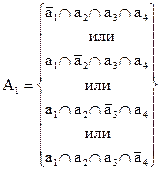(1.64)
 |
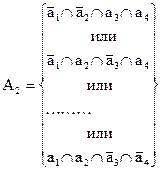(1.65)
Как видно из соотношений (1.63 – 1.65) все события в круглых скобках попарно несовместимы, так как каждое из них включает противоположное событие. Следовательно, и события будут несовместны. Поэтому соотношение (3.42) можно представить в виде
Н = Р(А0) + Р(А1) + Р(А2) (1.66)
Считая отказы отдельных двигателей независимыми событиями для вероятностей Р(Аi), получим
(1.67)
Для равнонадежных двигателей соотношение (1.67) запишутся так
 |
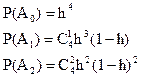(1.68)
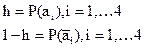где
(1.69)
Подставляя (1.68) в (1.66), окончательно получим
 |
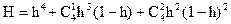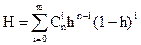Полученные результаты могут быть обобщены на общий случай. Пусть ДУ состоит из n одинаковых двигателей. Причем, для выполнения задачи достаточно иметь в исправном состоянии l блоков, а m = n – l находятся в «горячем» резерве. Тогда соотношение примет вид
(1.70)
Рассмотренный выше тип резервирования используется для повышения надежности двигательных установок. В частности, в ДУ первой ступени РН «Сатурн 1» допускался выход из строя одного из 8 ЖРД Н-1. При этом расчетное соотношение примет вид
НДУ = h8 + 8h7(1 – h)
где h = 0,965 – надежность одного двигателя.
После подстановки получим
НДУ = 0,75 + 0,21 = 0,96
В случае отсутствия резервного двигателя оценка надежности ДУ равны
НДУ,0 = h7 = 0,9657 = 0,78
Таким образом введение резервного двигателя позволяет существенно поднять уровень надежности ДУ.
Рассмотренный выше подход может быть использован так же для оценки надежности при мажоритарном резервировании, применяемом для повышения точности работы СУ.
