Схема гибели и размножения.
Таким образом имея в расположении размеченный граф состояний можно легко напасать уравнения Колмогорова для вероятностей состояний, а также написать и решить алгебраические уравнения для финальных вероятностей. Для некоторых случаев удается последние уравнениярешить заранее, в буквенном виде. В частности, это удается сделать, если граф состояний системы представляет собой так называемую «схему гибели и размножения» Граф состояний для схемы гибели и размножения имеет вид, показанный на рис.1.17.

Рис. 1.17 Граф схемы «гибели и размножения».
Особенность этого графа в том, что все состояния системы можно вытянуть в одну цепочку, в которой каждое из средних состояний (S1, S2, … Sn-1) связано, прямой и обратной стрелкой с каждым из соседних состоянии — правым и левым, а крайние состояния. (S0, Sn) —только с одним соседним состоянием. Термин «схема гибели и размножения» ведет, начало от биологических задач, где подобной схемой описывается изменение численности популяции.
Схема гибели и размножения очень часто встречается в разных задачах практики,, поэтому полезно, одни раз и навсегда, найти для нее финальные вероятности состояний.
Предположим, что все потоки событий, переводящие систему по стрелкам графа,— простейшие (для краткости будем называть и систему S и протекающий в ней процесс — простейшими).
Пользуясь графом рис.1.17 составим и решим алгебраические уравнения для финальных вероятностей состояний (их. существование вытекает из того, что из каждого состояния можно перейти в каждое другое) Для стояния S0 имеем:  .
.
Для второго состояния S1 :  .
.
Равенство приводится к виду  .
.
Далее, совершенно аналогично 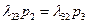 .
.
и вообще  , где к принимает все значения от 0 до n..
, где к принимает все значения от 0 до n..
Итак, финальные вероятности р0, р1 ,…, рnудовлетворяют уравнениям

Кроме того, надо учесть нормировочное условие

Решим эту систему уравнений из первого уравнения выразим р1через р0:
 .
.
Из второго, получим:  ,
,
из третьего 
и вообще, для любого k (от 1 до n)  .
.
Обратим внимание на то, что в выражении для  в числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данногo состояния Sk), а в знаменателе — произведение всех интенсивностей стоящих у стрелок, ведущих справа налево (с начала и до Sk)
в числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данногo состояния Sk), а в знаменателе — произведение всех интенсивностей стоящих у стрелок, ведущих справа налево (с начала и до Sk)
Таким образом, все вероятности состояний р0,... рп выражены черед одну из них (р0). Подставим эти выражения в нормировочное условие, вынося за скобку р0

Отсюда получим выражение для 

. Все остальные вероятности выражены через р0. Заметим, что коэффициенты при р0 в каждой из них представляют собой не что иное, как последовательные члены ряда, стоящего после единицы в формуле для  . Значит, вычисляя р0, мы уже нашли все эти коэффициенты Полученные формулы очень полезны при решении простейших задач теории надежности и массового обслуживания.
. Значит, вычисляя р0, мы уже нашли все эти коэффициенты Полученные формулы очень полезны при решении простейших задач теории надежности и массового обслуживания.
«Холодный» резерв с восстановлением отказавших элементов.
С учетом восстановления с неограниченными возможностями ремонта, граф состояний при «холодном» резерве примет вид, представленный на рис. 1.18.

Рис. 1.18 Граф состояний системы.
Для представленного графа получим  .
.
Вероятность  оценивается из условия нормировки
оценивается из условия нормировки  .
.
Таким образом окончательно получим
 (1.61)
(1.61)
«Горячий» резерв с восстановлением отказавших элементов.
Граф состояний для «горячего» резерва приведен на рис. 1.19.

Рис. 1.19 Граф состояний системы.
Для рассматриваемого графа имеем
 .
.
Производя преобразования, найдем
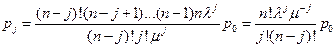
Из условия нормировки получим

Отсюда 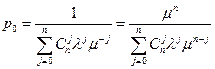
Таким образом окончательно найдем
 .
.






