Резервирование замещением в случае ненагруженного резерва

 

Пусть все k резервных элементов составляют ненагруженный резерв. В этом случае естественно считать, что резервный элемент не может отка­зать до его включения в работу. Поэтому введенные в подразд. 4.5 веро­ят­ности и 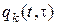здесь будут:

 

и , (2.72)

 

где р_k и q_k – надежность и ненадежность k -го резервного элемента в рабо­чем режиме. Учитывая это, основные рекуррентные формулы (2.58) и (2.59) запишем так:

 

(2.73)

 

(2.74)

 

Но пользоваться формулами (2.73), (2.74) неудобно, так как для вы­числения по этим формулам надежности и ненадежности k -кратно резервированной группы надо уже знать плотность распределе­ния времени безотказной работы (k -1)-кратно резервированной группы. Однако формулы (2.73), (2.74) можно упростить.

Обозначая , и применяя к интегралу фор­мулу интегрирования по частям, получаем:

 

 

 

 

(2.75)

 

где учитываем, что P_k (0) = 1, Q_{k –1}(0) = 0.

Аналогично можно преобразовать и формулу (2.74). Тогда ради уп­рощения, допуская, что все элементы в рассматриваемой резервированной группе равнонадежны, окончательно получаем:

 

(2.76)

(2.77)

 

где p (t), q (t), f (t) = – – количественные характеристики надежности, общие для всех элементов этой группы. Зная эти характеристики и приме­няя последовательно k раз рекуррентные формулы (2.76) и (2.77), получаем надежность P_k (t) и ненадежность Q_k (t) рассматриваемой резервированной группы в случае, когда ее элементы равнонадежны.

Рассмотрим практически важный частный случай, когда все эле­менты k -кратно резервированной группы (см. рис. 2.19) с ненагруженным резервированием подчинены одному и тому же экспоненциальному закону надежности: .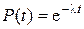

Тогда, учитывая равенство и применяя формулу (2.76), последовательно находят:

1) при k = 1

; (2.78)

 

2) при k = 2

(2.79)

 

3) при k = 3

(2.80)

И в случае любого k получаем:

 

(2.81)

 

Пользуясь этой формулой, можно найти и все другие количествен­ные характеристики надежности рассматриваемой резервированной группы.

Ненагруженное резервирование замещением обеспечивает большую надежность, чем нагруженное резервирование. Это очевидно, так как во втором случае в отличие от первого расход надежности резерва начинается сразу же после включения системы в работу.

Резервирование замещением наряду с нагруженным резервом позво­ляет также использовать облегченный и ненагруженный резервы. В этом состоит его преимущество перед резервированием с постоянным включе­нием резерва, которое позволяет использовать только нагруженный резерв.