Расчет надежности системы при резервировании замещением

 

Если по условиям выполняемого задания работу системы можно прерывать для замены отказавшего элемента резервным, то обычно при­меняют резервирование замещением отказавшего элемента. Особенность этого резервирования состоит в том, что резервный элемент включается в работу только после отказа основного, а до этого он содержится в резерве и непосредственно в работе не участвует.

Чтобы резервный элемент в момент его включения в работу был подготовлен к выполнению этой работы, иногда его приходится содержать в резерве в некотором нагруженном режиме. В общем случае резервный элемент до его включения в работу может содержаться в резерве в одном из следующих состояний:

– в том же самом рабочем режиме, что и работающий основной (на­груженный резерв);

– в облегченном рабочем режиме (облегченный резерв);

– в ненагруженном режиме (ненагруженный резерв).

Рассмотрим сначала случай резервирования замещением одного ос­новного элемента 0 одним дублирующим 1, который переключающим уст­ройством П₁ включается в работу в момент отказа основного (рис. 2.17).

Рис. 2.17. Резервированная группа Рис. 2.18. Функция плотности распределения

резервированной группы

Пусть график плотности распределения времени безотказной работы основного элемента 0 имеет такой вид резервированной группы, где отре­зок времени t разделен на n частичных отрезков D t_i º t_i – t_{i –1}, i = 1, 2, …, n (рис. 2.18).

Тогда рассматриваемая резервированная группа (см. рис. 2.17) к мо­менту времени t не откажет лишь в случаях, когда:

1) либо основной элемент 0 к моменту t не откажет;

2) либо основной элемент 0 откажет к моменту , где t_{i –1} < < t_i < t, i = 1, 2, …, n, но резервный элемент 1, будучи исправным к времени < t, не откажет на отрезке времени t – .

Принимая отказы основного элемента 0 на отрезках времени D t_i º t_i – – t_{i –1}, i = 1, 2, …, n за гипотезы, по формуле полной вероятности получаем:

 

(2.52)

 

где Р ₁(t) – надежность рассматриваемой резервированной группы (см. рис. 2.17); Р ₀(t) – надежность основного элемента 0; – вероятность гипотезы отказа основного элемента 0 на отрезке вре­мени D t_i; – вероятность безотказной работы резервного элемента 1 к моменту t при условии, что основной элемент отказал в момент .

Переходя в формуле к пределу max D t Þ 0, получим точное выраже­ние для надежности Р ₁(t) рассматриваемой резервированной группы:

 

(2.53)

 

Формула, естественно, обобщается на случай k -кратного резервиро­вания замещением, т.е. такого резервирования, когда в момент отказа ос­новного элемента 0 переключающее устройство П₁ включает в работу 1-й резервный элемент, в момент отказа 1-го резервного элемента переклю­чающее устройство П₂ включает 2-й резервный элемент и т.д. до включе­ния в работу последнего k -кратного резервного элемента. Такую группу элементов k -кратного резервирования можно рассматривать как группу элементов, составленную из группы (k – 1)-кратного резервирова­ния и од­ного дополнительного k -го резервного элемента (рис. 2.19). При таком рас­смотрении формула для k -кратно резервированной группы при­мет вид

 

(2.54)

где – надежность рассматриваемой группы k -кратного резервирова­ния; 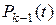– надежность группы (k –1)-кратного резервирования; – вероятность безотказной работы k -го резервного элемента к мо­менту времени t при условии, что группа (k –1)-кратного резервирования отказала в момент t; 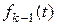– плотность распределения времени безотказ­ной работы группы (k –1)-кратного резервирования.

Рис. 2.19. k -кратное резервирование

 

Если обозначить через 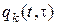– вероятность того, что k -й резервный элемент откажет к моменту t при условии, что группа (k –1)-кратного ре­зервирования отказала в момент t, т.е. если

 

(2.55)

 

то формулу можно переписать так:

 

(2.56)

Но

 

и , (2.57)

где 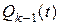– надежность (k –1)-кратно резервированной группы. Поэтому

 

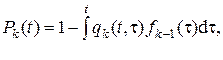(2.58)

откуда окончательно получим:

 

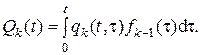(2.59)

 

Эти формулы и являются основными формулами расчета надежности системы при резервировании замещением.

При выводе этих формул мы допускали, что переключающие уст­ройства П₁, П₂, …, П _k действуют безотказно. Однако надежность этих пе­реключающих устройств легче учесть, рассматривая их как самостоятель­ные элементы, включенные последовательно с соответствующими резерв­ными элементами группы.

В следующих трех подразделах рассмотрим частные случаи резерви­рования замещением: нагруженный, облегченный и ненагруженный ре­зервы.