В данном параграфе будет изложена методика расчета сложных систем при постоянно включенном резерве с использованием структурно-логических схем надежности (СЛСН) и структурно-логических функций надежности (СЛФН), которые строятся по структурной или структурно-функциональной схеме системы. В конце раздела будет показано, как использовать марковские цепи для построения СЛФН системы.
В расчетах будет допускаться, что элементы системы в смысле надежности независимы, т.е. отказы одних элементов не изменяют надежности других. Однако, в общем случае, это довольно грубое допущение, так как на самом деле элементы в системе обычно зависимы. Например, отказ одного из двух элементов, включенных параллельно, может изменить надежность оставшегося, так как последний вследствие этого может оказаться более нагруженным.
Чтобы учесть зависимость между элементами, надо при расчете надежности исходить не из абсолютных значений надежности составляющих элементов, а из условных надежностей, вычисленных при различных условиях отказа того или иного числа элементов системы. Однако это приводит к резкому усложнению методики, и в данном учебном пособии такой подход не используется.
Методику расчета сложных систем с постоянно включенным резервом удобнее всего изложить, используя конкретные примеры. Рассмотрим, как одну из возможных, структурную схему технической системы, приведенную на рис. 2.12.
Это вариант системы с функциональным резервированием. Собственно система состоит из сервера и удаленного персонального компьютера. Для повышения надежности сервер задублирован (блоки С3 и С4 на рис. 2.12), персональный компьютер также (блоки ПК1 и ПК2 на рис. 2.12). Кроме того, благодаря коммутатору К5 возможен доступ от любого персонального компьютера к параллельно подключенному варианту сервера. Покажем, как для данной системы использовать логико-вероятностный метод расчета надежности.
 |
Рис. 2.12. Структура системы с функциональным резервированием
Алгоритм будет выглядеть следующим образом:
1. На первом этапе строим СЛСН. Она приведена на рис. 2.13. Основными являются блоки 1 и 3. Блоки 2 и 4 их дублируют. Блок 5 одновременно резервирует часть функций блоков 3 и 4. Получается мостиковая схема, в которой нет возможности выделить параллельное и последовательное соединение.
 |
Рис. 2.13. Структурно-логическая схема надежности
2. На втором этапе по СЛСН строим СЛФН. Введем понятие истока (точка, в которой сигнал поступает в схему) и стока (точка выхода сигнала из схемы). Для построения СЛФН необходимо включить в нее все возможные пути от истока до стока. Для рассматриваемой схемы (см. рис. 2.13) словесная формулировка работоспособности будет записана следующим образом: объект работоспособен, если исправны блоки 1 и 3 или блоки 2 и 4, или блоки 1, 5 и 4, или блоки 2, 5 и 3.
3. Записываем структурно-логическую функцию надежности:
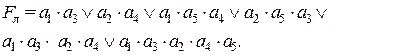(2.32)
4. Минимизация логической функции. Минимизация логической функции проводится любыми известными из теории логической алгебры способами. После минимизации функция примет вид
5. Упрощение логической функции. Функцию стараются привести к такому виду, чтобы в каждую функцию входило не больше двух членов. Для этого можно воспользоваться разложением функции по какой-либо переменной на две части. Данное разложение в общем виде выглядит следующим образом [2]:
(2.33)
Используем (2.33) для преобразования полученной на втором этапе СЛФН:
6. Арифметизация булевой функции. Правила арифметической функции следующие:
(2.34)
a & b = ab, (2.35)
= 1 – a, (2.36)
Fa = a 5[ a 1 + a 2 – a 2 × a 1)(a 3 + a 4 – a 3 × a 4)] + (1 – a 5)(a 1 × a 3 + a 2 × a 4 –
– a 1 × a 3 × a 2 × a 4) – a 5(1 – a 5)(a 1 + a 2 – a 2 × a 1)(a 3 + a 1 – a 3 × a 4)(a 1 × a 3 +
+ a 2 × a 4 – a 1 × a 2× a 3 × a 4). (2.37)
7. Замена событий их вероятностями:
Pc = P 5(P 1 + P 2 – P 1 × P 2) + (1 + P 5)(P 1 × P 3 + P 2 × P 4 –
– P 1 × P 3 × P 2 × P 4) – P 5(1 – P 5)(P 1 + P 2 – P 2 × P 1)(P 1 × P 3 +
+ P 2 × P 4 – P 1 × P 2× P 3 × P 4). (2.38)
8. Расчет надежности.
Пусть Р 1 = Р 2 = 0,9; Р 3 = Р 4 = Р 5 = 0,8; Р с = 0,8(0,9 + 0,9 +
+ 0,64) + 0,1(0,9 × 0,8 + 0,9 × 0,8 – 0,64 × 0,81) – 0,8 × 0,1(0,9 + 0,9 –
– 0,64)(0,8 + 0,8 – 0,64)(0,72 + 0,72 – 0,64 × 0,81) = 0,938. (2.39)
Если СЛСН системы можно свести только к последовательному и параллельному соединению участков, то расчет надежности можно упростить.
Рассмотрим СЛСН, приведенную на рис. 2.14.
Рис. 2.14. Структурно-логическая схема надежности
1. Словесная формулировка условий работоспособности объекта. Для приведенной схемы: объект исправен, если исправны блоки 1, 3 и 4 или блоки 2, 3 и 4.
2. Составление структурно-логической функции надежности:
. (2.40)
3. Минимизация и упрощение логической функции:
(2.41)
4. Арифметизация булевой функции:
(2.42)
5. Замена событий их вероятностями:
(2.43)
Однако
(2.44)
т.е. мы видим, что для блоков 1 и 2, соединенных параллельно, мы пришли к формуле расчета надежности при параллельном соединении (1.20) (подразд. 1.2.3), а для последовательного соединения: параллельный участок (блок 1 –блок 2), блок 3, блок 4 мы пришли к формуле расчета надежности при последовательном соединении (1.17) (подразд. 1.2.2).
Таким образом, задача расчета надежности свелась к поэтапному выделению последовательных и параллельных участков и применению формул (1.20) и (1.17). Покажем применение этого упрощенного метода на примере СЛСН, приведенной на рис. 2.15.
 |
Рис. 2.15. Структурно-логическая схема надежности
Здесь основными являются блоки 1, 3, 4, 8. Блок 1 является самым ненадежным и резервируется однотипным ему блоком 2. Подсистема блоков 1, 2, 3, 4 также не является достаточно надежной и потому функционально резервируется подсистемой блоков 5, 6, 7, в которой блоки 5 и 6 – однотипные с низкими надежностными показателями. Блок 8 является высоконадежным и не требует резервирования.
Пусть
Р 1 = Р 2 = 0,8, Р 3 = 0,9, Р 4 = 0,9,
Р 5 = Р 6 = 0,82, Р 7 = 0,85, Р 8 = 0,99.
Обозначим выделенные участки римскими цифрами:
(2.45)
(2.46)
(2.47)
(2.48)
(2.49)
(2.50)
Сравним полученную надежность с надежностью нерезервированной системы:
(2.51)
Следует учесть, что построить СЛСН для сложных систем, особенно при наличии функционального резервирования, не всегда просто. Желательно иметь формальный алгоритм для построения СЛФН, использующий другие методы и структуры. Такой алгоритм будет использовать в качестве математического аппарата марковские цепи [2]. Покажем, как строится марковская цепь для технической системы, приведенной на рис. 2.12.
Сначала выпишем все возможные состояния системы:
0 – все блоки исправны, система работоспособна;
1 – блок 1 неисправен, система работоспособна;
2 – блок 2 неисправен, система работоспособна;
…
5 – блок 5 неисправен, система работоспособна;
6 – блоки 1 и 2 неисправны, система неработоспособна:
7 – блоки 1 и 3 неисправны, система неработоспособна;
…
32 – все блоки неисправны, система неработоспособна.
Будем считать, что два события одновременно произойти не могут, т.е. из состояния 0 мы можем попасть в состояние с одним отказавшим блоком (состояния 1–5), но не с двумя или больше. Марковская цепь для рассматриваемой системы приведена на рис. 2.16. Внутри каждого состояния проставлены неисправные блоки, каждое состояние помечено либо как «р» (работоспособное), либо как «н/р» (неработоспособное).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.16. Марковская цепь для системы с функциональным резервированием
Теперь по этой марковской цепи можно непосредственно записать минимизированную СЛФН. Очевидно, что в СЛФН могут войти только состояния, в которых система работоспособна.
Начиная от конца схемы, просматриваем состояния, пока не найдем состояние, помеченное как работоспособное. По нашей цепи это состояние с неисправными блоками 1, 3 и 5, т.е. с исправными блоками 2 и 4. Вносим в СЛНФ терм a 2 a 4. Затем вычеркиваем из кандидатов на внесение в СЛФН предшественников выбранного нами состояния (т.е. состояний, из которых мы могли попасть в данное состояние) вплоть до состояния 0. Для рассматриваемого состояний это будут: состояние с неисправными блоками 1 и 3, состояние с неисправными блоками 1 и 5, состояние с неисправными блоками 3 и 5, состояние с неисправным блоком 1, состояние с неисправным блоком 3, состояние с неисправным блоком 5 и состояние со всеми исправными блоками.
Процесс повторяем до тех пор, пока все состояния, в которых система работоспособна, либо войдут в СЛФН, либо будут вычеркнуты.
Легко увидеть, что по завершении работы алгоритма мы получим:
т.е. ту же функцию, что при составлении СЛФН по СЛСН.
Недостаток метода – большая размерность марковской цепи, однако при использовании данного алгоритма мы гарантированно получаем правильную минимизированную СЛФН.
