Пусть все k резервных элементов составляют облегченный резерв. В этом случае, как и при нагруженном резерве, отказ резервного элемента может наступить и до его включения в работу. Поэтому введенную выше вероятность безотказной работы k -го резервного элемента 
здесь можно представить так:
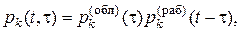(2.65)
где 
– надежность k -го резервного элемента в облегченном режиме, т.е. в резерве, а 
– надежность этого же k -го резервного элемента в рабочем режиме при условии, что до включения в работу он, будучи в резерве, не откажет к моменту t.
Учитывая это выражение, основные рекуррентные формулы (2.58) и (2.59) перепишем так:
(2.66)
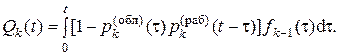(2.67)
Рассмотрим практически важный частный случай, когда все элементы k -кратно резервированной группы (см. рис. 2.19) с облегченным резервированием подчинены экспоненциальному закону надежности. Пусть
(2.68)
Тогда из формулы (2.66) последовательно найдем:
1) при k = 1
; (2.69)
2) при k = 2
(2.70)
Проведя подобные вычисления для k = 3, 4, …, находим закономерность изменения Pk (t), согласно которой
. (2.71)
Пользуясь этой формулой, можно найти и все другие количественные характеристики надежности рассматриваемой резервированной группы.
