Пусть все k резервных элементов составляют нагруженный резерв. В этом случае
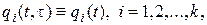(2.60)
где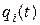 
– ненадежность i -го резервного элемента.
Тогда формула (2.59) примет вид:
(2.61)
Применяя k раз найденное рекуррентное соотношение
(2.62)
получаем ту же формулу, что и в случае нагруженного резерва с постоянным включением резервных элементов в работу (подразд. 2.2.3):
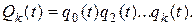(2.63)
Этот результат очевиден, так как случаи нагруженного резервирования с постоянным включением и замещением в смысле надежности не отличаются друг от друга. Действительно, в обоих случаях расход надежности всех резервных элементов начинается с момента включения системы в работу и протекает одинаково интенсивно. Для экспоненциального закона распределения
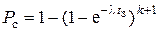. (2.64)
