Расчет надежности по графу работоспособности объекта

Исследование надежности восстанавливаемых объектов требует привлечения аппарата случайных процессов, описывающих процессы перехода изделия из одного состояния в другое в случайные моменты времени. Эти данные расчета отличаются от расчетов надежности невосстанавливаемых объектов, где достаточно теории случайных событий и величин.

Ниже рассматриваются по этапам наиболее иллюстрированный метод расчета надежности, основанный на составлении графа переходов изделия в различные состояния работоспособности.

На первом этапе составляется граф работоспособности объекта. Для этого определяются все состояния работоспособности с учетом блоков системы и устанавливаются интенсивности переходов по данным состояниям. Например, для системы с восстановлением из двух блоков (рис. 2.21), один из которых резервный, могут быть выделены следующие состояния:

1. Блок 1 и блок 2 исправны (система полностью исправна).

2. Блок 1 отказал, блок 2 исправен.

3. Блок 2 отказал, блок 1 исправен.

4. Отказ блока 1 и блока 2 (отказ системы).

Вероятность нахождения системы в i -м выделенном состоянии обозначается Р_i. Вероятность перехода из i состояния в j – Р_ij. Например, Р ₁₂ – вероятность отказа первого блока, Р ₂₁ – вероятность восстановления первого блока и т.д.

Граф работоспособности системы (см. рис. 2.21), построенный с учетом введенных обозначений, представлен на рис. 2.22.

Рис. 2.21. Структура системы Рис. 2.22. Граф работоспособности системы

с параллельным соединением

Граф переходов по состояниям можно представить также матрицей переходов, используемой в дальнейшем для автоматизации расчетов:

Как видно из определений, граф переходов аналогичен марковской цепи [2].

Вероятности вследствие ординарности потока равны нулю.

Система уравнений, определяющая вероятности состояний, имеет следующий вид:

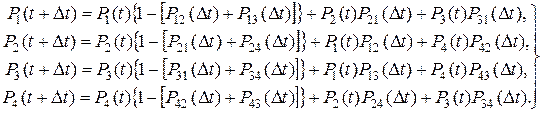(2.101)

Уравнения системы, например первое, читается следующим образом: вероятность того, что система во время t + D t будет находиться в первом состоянии, равна произведению вероятности того, что система в момент времени t находилась в первом состоянии, и вероятности отсутствия перехода во второе и третье состояние, плюс вероятности того, что система находилась во втором или третьем состоянии в момент t, умноженные на вероятности перехода из этих состояний в первое за промежуток D t.

Если D t достаточно мало, то 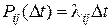, где 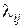– интенсивность перехода из i -го состояния в j -е состояние.

Система, записанная в функциях интенсивностей, имеет следующий вид:

(2.102)

Перенос везде 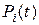влево и деление уравнений на D t приводит к получению в левой части:

(2.103)

При условии D t Þ 0 получаем:

(2.104)

В окончательном виде система описывается следующими дифференциальными уравнениями:

(2.105)

При расчетах надежности систему уравнений составляют по графу работоспособности сразу в виде (2.105), минуя рассмотренные пояснительные этапы. Существует следующее правило составления системы. В левой части каждого уравнения записывается . В правой части уравнения содержится столько членов, сколько стрелок связано (входит и выходит) с данным состоянием. Каждый член равен произведению интенсивности потока l, переводящего систему по данной стрелке, умноженной на вероятность того состояния, откуда стрелка исходит. Если стрелка входит в описываемое состояние, то произведению присваивается знак «+», если исходит, то знак «–».

Приведенное правило позволяет после получения графа работоспособности изделия составить систему дифференциальных уравнений, описывающих функционирование объекта.

На втором этапе в соответствии с приведенным правилом по графу работоспособности изделия составить систему дифференциальных уравнений, описывающих функционирование объекта.

На третьем этапе решаются уравнения системы и находятся искомые вероятности пребывания объекта в состояниях его работоспособности. Очевидно, что в рассматриваемом примере коэффициент готовности равен вероятности застать ответ в одном из трех работоспособных состояний:

(2.106)

Решение системы может быть выполнено известными способами. В дальнейшем используется способ, основанный на преобразованиях Лапласа, переводящих систему дифференциальных уравнений в систему алгебраических уравнений:

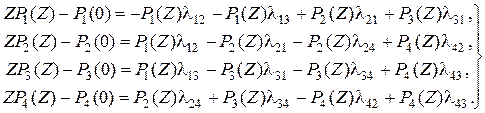(2.107)

Из системы алгебраических уравнений находятся вероятности пребывания системы в состояниях . С помощью обратных преобразователей Лапласа полученные вероятности приводят к искомому виду .

В случаях когда вероятности состояний являются постоянными, что характерно для установившегося режима работы, достигаемого в практике сравнительно быстро при существующих соотношениях и , система уравнений (2.105) становится системой алгебраических уравнений, так как в этом случае = 0.

(2.108)

Добавление последнего уравнения является обязательным и необходимым для закрытия системы, поскольку ни одно из предыдущих уравнений не учитывает начальных условий.

Решение системы (2.108) позволяет определить установившийся коэффициент готовности. Рассмотрим порядок расчета на более конкретном примере.

Пример 2.6. Пусть необходимо определить надежность изделия, не имеющего резервирования, с заданными интенсивностями переходов – параметров потока отказов w = const и интенсивностью восстановления m. Работоспособность системы описывается графом (рис. 2.23): состояние 1 – состояние работоспособности, состояние 2 – состояние отказа.

Описание графа по приведенному правилу дает следующую систему уравнений вида (2.107):

Учитывая, что в момент включения t = 0 система должна быть исправна (), получаем:

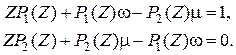
Отсюда

(2.109)

Обратное преобразование вероятности требует приведения ее к табличному виду. Для этого умножим и разделим на (w + m):

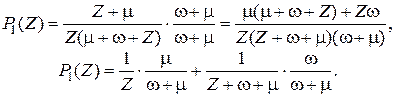
Отсюда, учитывая, что 1/ Z соответствует 1(t), а соответствует , получаем:

(2.110)

Анализом полученного выражения устанавливаем, что при t Þ¥ не может быть ниже величины . Эта постоянная часть и является стационарным коэффициентом готовности изделия:

(2.111)

Постоянная времени экспоненты . Переходный процесс длится 3¸4 Т _пэ, после чего наступает установившийся режим.

Пример 2.7. Пусть w= 10^–2 1/ч, а m = 1 1/ч. Тогда

ч.

Следовательно, переходный процесс длится 3¸4 ч, а далее надежность системы определяется стационарным коэффициентом готовности:

На рис. 2.24 приведен график зависимости коэффициента готовности от времени.

Рис. 2.24. График зависимости коэффициента готовности от времени

2.3.3. Определение среднего времени наработки на отказ системы с восстановлением

Время наработки на отказ (подразд. 2.1.1) определяется как

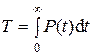В то же время преобразование Лапласа определяется следующей формулой [2]:

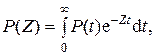(2.112)

т.е. при Z = 0 Т = P (Z).

Рассмотрим систему из двух восстанавливаемых блоков, один из которых основной, а другой – резервный. Перепишем систему уравнений (2.107), заменяя на 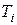, с учетом того, что состояние 4 – состояние отказа. В результате , а также исчезает строка, соответствующая ,

(2.113)

Среднее время наработки на отказ всей системы 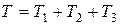, так как 1, 2, 3 – состояния работоспособности.

Пример 2.8. Пусть

Тогда

Решив систему, получаем:

Среднее время наработки на отказ

ч.

2.3.4. Расчет надежности систем с восстановлением при основном (последовательном) и параллельном соединении элементов

Рассмотрим методику, приведенную в подразд. 2.3.2, для различных видов соединения элементов. Возьмем систему, состоящую из двух образцов оборудования, соединенных последовательно так, что отказ любого из них приводит к отказу всей системы (рис. 2.25). Для простоты предположим, что каждый образец имеет одинаковую интенсивность отказов w и интенсивность ремонтов m.

Предположим, что у нас имеется один ремонтник. Составим граф переходов системы (рис. 2.26).

Рис. 2.25. Структура системы Рис. 2.26. Граф работоспособности системы

с последовательным соединением

Обозначим:

0 – состояние системы, в котором оба образца исправны;

1 – состояние системы, когда один образец исправен, а другой ремонтируется;

2 – состояние системы, когда оба образца неисправны, один ремонтируется.

Из состояния 0 система может перейти в состояние 1 с интенсивностью отказов 2w. Из состояния 1 система может перейти в состояние 0 с интенсивностью восстановления m и в состояние 2 с интенсивностью отказов w. Из состояния 2 система может перейти в состояние 1 с интенсивностью восстановления m.

Запишем по графу переходов систему дифференциальных уравнений:

(2.114)

Будем искать решение только для установившегося значения. Тогда система дифференциальных уравнений перейдет в систему линейных уравнений:

(2.115)

Отсюда коэффициент готовности

(2.116)

Пример 2.9. Пусть w = 10² 1/ч, m = 1 1/ч. Определить коэффициент готовности:

В общем случае, если у нас имеется n образцов оборудования и один ремонтник, справедлива формула:

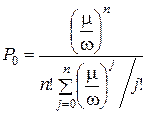. (2.117)

В качестве другого крайнего случая рассмотрим систему, когда количество ремонтников равно количеству образцов оборудования. Пусть на оба образца имеется два ремонтника. Составим граф перехода системы (рис. 2.27):

0 – состояние системы, в котором оба образца исправны;

1 – состояние системы, когда один образец исправен, а другой ремонтируется;

2 – оба образца неисправны и ремонтируются.

Рис. 2.27. Граф переходов системы

Запишем по графу переходов систему уравнений для установившегося значения:

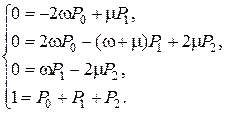
Решая систему, получим:

(2.118)

Пример 2.10. Пусть w= 10^–2 1/ч, m = 1 1/ч. Определить коэффициент готовности:

В общем случае, если у нас имеется n образцов оборудования и n ремонтников,

(2.119)

т.е. коэффициент готовности системы находится как произведение коэффициентов готовности каждого образца. Это и следовало ожидать, так как для каждого образца имеется свой ремонтник и K _г каждого образца не зависит от K _г остальных.

Рассмотрим систему из двух образцов оборудования, соединенных параллельно (рис. 2.28). Как уже указывалось, в этом случае отказ системы наступает только при отказе всех элементов системы.

Предположим, что у нас имеется один ремонтник, который сразу начинает ремонтировать отказавший элемент.

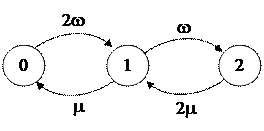
Составим граф переходов системы (рис. 2.29):

0 – состояние системы, в котором оба образца исправны;

1 – состояние системы, когда один образец исправен, а другой ремонтируется;

2 – оба образца неисправны, один ремонтируется.

Рис. 2.28. Структура системы Рис. 2.29. Граф переходов системы

с параллельным соединением

Запишем по графу переходов систему уравнений для установившегося значения:

Решив систему, получим:

Коэффициент готовности

(2.120)

Пример 2.11. Пусть w = 10^–2 1/ч, m = 1 1/ч. Определить коэффициент готовности:

Имеется довольно многочисленный класс систем, в которых обслуживание невозможно начать до наступления полного отказа системы. Это может произойти, если контролируется только выход из строя всей системы, а не отдельных образцов оборудования. Допустим, у нас имеется 2 образца оборудования, соединенных параллельно. После того как откажет вся система, два ремонтника начинают ремонтировать каждый свой элемент.

Составим граф переходов системы (рис. 2.30):

0 – состояние системы, в котором оба образца исправны;

1 – состояние системы, когда один образец исправен, а другой неисправен, но не ремонтируется;

2 – состояние системы, когда оба образца неисправны и ремонтируются.

Рис. 2.30. Граф переходов системы

Запишем по графу переходов систему уравнений для установившегося значения:

Решив систему, получим:

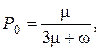
Коэффициент готовности:

(2.121)

Пример 2.12. Пусть w = 10^–2 1/ч, m = 1 1/ч. Определить коэффициент готовности:

В данном разделе мы рассмотрели несколько вариантов расчета стационарного коэффициента готовности для систем с последовательным и параллельным соединением однотипных элементов. В случае параллельного соединения однотипных элементов коэффициент готовности при тех же параметрах потока отказов и восстановлений значительно выше, так как параллельное соединение одинаковых элементов означает наличие резервирования.

Однако примеры были выбраны минимальной размерности. Для реальных систем количество блоков будет значительно большим, параметры потока отказов и восстановлений – различными. Все это приводит к тому, что размерность графа переходов системы, как правило, оказывается чрезмерно большой для практических расчетов. В этих случаях граф можно сократить, отбросив состояния, вероятность пребывания в которых пренебрежимо мало. Технология сокращения графа переходов системы проиллюстрирована ниже на двух реальных примерах расчета надежности сложной телекоммуникационной системы.