1) Объем выборки равен 
. Выборочное среднее и дисперсия определяются по формулам (1.2), (1.3)
;
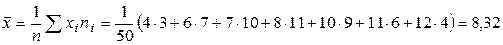Исправленная выборочная дисперсия равна 
.
Исправленное среднее квадратичное отклонение будет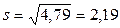 
.
2) Доверительный интервал для математического ожидания найдем по формуле (1.4). Значение 
определим из таблицы по доверительной вероятности 
и объему выборки 
: 
. Тогда доверительный интервал имеет вид:
.
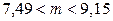Доверительный интервал для дисперсии определим по формуле (1.5): 
(
). Тогда границы интервала принимают вид:
; 
, т.е.
.
3) Размах варьирования находится по формуле 
. Среднее абсолютное отклонение
;
.
4) Вычислим медиану и моду. Так как 
, значит
.
Мода 
.
5) Согласно определению эмпирической функции распределения, ее значение при любом 
равно 
, где 
– количество элементов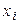 
выборки, меньших чем .
Например, при 
имеем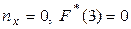 
;
при 
;
при 
;
при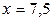 
;
при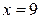 
;
при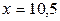 
;
при 
;
при 
.
Итак, эмпирическая функция распределения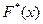 
имеет вид:
6) Из статистического ряда видно, что 
, 
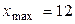, поэтому 
. Границы интервалов будут 
; 
. Частота 
интервала 
подсчитывается с помощью ряда как число наблюдений, попавших в интервал. Так в первый 
интервал 
попало 3 значения, во второй 
- 7+10=17 значений. Аналогично, 
. Сведем полученные данные в таблицу:
| 4 – 5.6 | 5.6 – 7.2 | 7.2 – 8.8 | 8.8 – 10.4 | 10.4 - 12 |
|
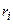
Найдем точечные оценки асимметрии и эксцесса. Применим формулы (7), предварительно вычислив величины 
: 
, 
, 
, 
, 
.
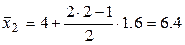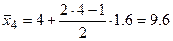Отсюда 
;
Теперь по формулам (1.8) вычислим их средние квадратичные ошибки:
, 
.
Так как 
(0.012<0.99) и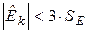 
(1.78<1.86), то можно сделать предположение, что гипотеза о нормальном распределении СВ 
может быть принята.
Проверим данное утверждение с помощью критерия согласия Пирсона. Найдем теоретические вероятности 
по формуле
,
где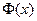 
– функция Лапласа, значения которой взяты из приложения (табл. П1). Результаты вычислений сведем в таблицу:
| 
| 
| 
| 
| 
| 
| 
| 
|
|
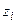
| 5.6 | – | -2,72 | – | -1,26 | -0,5 | -0,3962 | 0,1038 | ||
| 5.6 | 7.2 | -2,72 | -1,12 | -1,26 | -0,53 | -0,3962 | -0,2019 | 0,1943 | |
| 7.2 | 8.8 | -1,12 | 0,48 | -0,52 | 0,22 | -0,2019 | 0,0871 | 0,289 | |
| 8.8 | 10.4 | 0,48 | 2,08 | 0,22 | 0,96 | 0,0871 | 0,3315 | 0,2444 | |
| 10.4 | 2,08 | – | 0,96 | – | 0,3315 | 0,5 | 0,1685 |
Найдем теоретические частоты 
. Получим столбец:
|
| 5,19 |
| 9,715 |
| 14,45 |
| 12,22 |
| 8,425 |
Вычислим наблюдаемое значение критерия Пирсона. Для этого составим следующую расчетную таблицу:
|
| 
|
| 
| 
| 
|
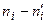
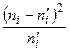
| 5,19 | -2,19 | 4,7961 | 0,924 | ||
| 9,715 | 7,285 | 53,07123 | 5,463 | ||
| 14,45 | -3,45 | 11,9025 | 0,824 | ||
| 12,22 | -3,22 | 10,3684 | 0,848 | ||
| 8,425 | 1,575 | 2,480625 | 0,294 | ||
| 8,354 |
По таблице критических точек распределения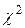 
, уровню значимости 
и числу степеней свободы 
находим 
. Так как 
, то гипотеза о нормальном распределении принимается.
