Выборочный коэффициент корреляции определяется равенством
, (2.4)
где 
– варианты (наблюдавшиеся значения) признаков 
и 
; 
– частота пары варианта 
; 
– объем выборки (сумма всех частот); 
– выборочные средние квадратические отклонения;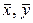 
– выборочные средние.
Известно, что если величины и независимы, то коэффициент корреляции r = 0; если 
, то и связаны линейной функциональной зависимостью. Следовательно, что коэффициент корреляции 
измеряет силу линейной связи между и .
Выборочный коэффициент корреляции 
является оценкой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами – количественными признаками и . Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или о равенстве нулю коэффициента корреляции генеральной совокупности). Если гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины и коррелированны; если гипотеза принята, то выборочный коэффициент корреляции незначим, а величины и не коррелированны.
Для того, чтобы при уровне значимости 
проверить гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины, надо вычислить наблюдаемое значение критерия
, (2.5)
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы 
найти критическую точку 
двусторонней критической области. Если 
, тогда нет оснований отвергать гипотезу. Если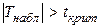 
, то гипотезу отвергают.
Пример 2. По данным примера 1 вычислить выборочный коэффициент корреляции и при уровне значимости 0.05 проверить гипотезу о равенстве нулю генерального коэффициента корреляции.
| x | -2 | -1 | ||||
| y | -0,4 | 0,2 | 0,7 | 1,6 | 2,0 | 3,5 |
По данным примера 
, 
для всех 
и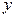 
. Найдем выборочные средние 
и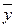 
и средние квадратические отклонения 
.
, 
;
, 
.
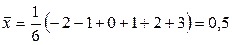Найдем 
и 
.
,
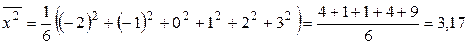Тогда 
, 
.
Выборочное значение коэффициента корреляции вычислим по формуле (2.4):
.
Проверим значимость полученного выборочного коэффициента корреляции. Найдем наблюдаемое значение критерия
По таблице критических точек распределения Стьюдента по уровню значимости 0.05 и числу степеней свободы 4 находим критическую точку двусторонней критической области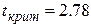 
.
Так как 
, то отвергаем гипотезу о равенстве нулю генерального коэффициента корреляцию, значит, и коррелированны.
