При обработке экспериментальных данных, при решении многих практических задач для характеристики свойств наблюдаемых случайных величин (СВ) и для проведения теоретических выкладок приходится делать предположение о виде законов распределения этих величин (нормальном, показательном, Пуассона, биномиальном и т.д.) или о соотношении между параметрами распределений. Такие предположения называют гипотезами. Приняв гипотезу, из нее получают определенные теоретические данные и проверяют, насколько они согласуются с результатами опыта.
Выбор распределения по опытным данным может быть сделан из следующих соображений:
· исходя из физической природы исследуемого объекта;
· по виду гистограммы или полигона относительных частот;
· по опытным данным ранее проведенных исследований;
· с помощью графического представления эмпирической функции;
· с помощью критериев согласия и т.д.
Нормальное распределение задается функцией, называемой плотностью распределения вероятности
(1.1)
где 
– математическое ожидание СВ 
;
– среднее квадратичное отклонение СВ .
Таким образом, нормальное распределение СВ определяется двумя параметрами: 
и 
, где 
– дисперсия СВ ( 
).
График плотности вероятности называется нормальной кривой (кривой Гаусса). СВ 
называют стандартизированной нормальной величиной.
Пусть при проведении 
опытов некоторая СВ Х принимает значения 
. Выдвинуто предположение, что СВ , причем и неизвестны. Для построения теоретико-вероятностной модели необходимо на основании выборки оценить математическое ожидание и среднее квадратичное отклонение .
Изучение случайных величин обычно начинают с группировки статистических данных, и.е. с разбиения интервала наблюдаемых значений СВ на 
подынтервалов равной длины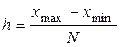 
и подсчета эмпирических частот 
, 
попадания значений СВ в соответствующие подынтервалы. Обычно 
.
