Пусть изучается система количественных признаков 
. В результате 
независимых опытов получены 
пар чисел 
Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии. Для определенности будем искать уравнение регрессии 
на 
:
.
Поскольку различные значения 
признака и соответствующие им значения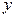 
признака наблюдались по одному разу, то группировать данные нет необходимости. Также нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так:
.
Угловой коэффициент прямой линии регрессии 
на 
называют выборочным коэффициентом регрессии на и обозначают через 
; он является оценкой коэффициента регрессии 
.
Итак, будем искать выборочное уравнение прямой линии регрессии на вида
(2.1)
Подберем параметры 
и b так, чтобы точки 
, построенные по данным наблюдений, на плоскости 
лежали как можно ближе к прямой. Уточним смысл этого требования. Назовем отклонением разность
, 
,
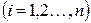где 
– вычисленная по уравнению (2.1) ордината, соответствующая наблюдаемому значению 
– наблюдаемая ордината, соответствующая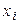 
.
Подберем параметры 
и b так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция 
этих параметров (временно вместо будем писать 
):
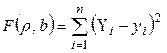, или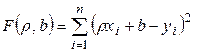 
.
Для отыскивания минимума приравняем нулю соответствующие частные производные:
, 
.
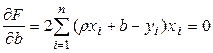Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно и 
:
; 
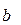(2.2)
Решив эту систему, найдем искомые параметры:
(2.3)
Аналогично можно найти выборочное уравнение прямой линии регрессии на :
,
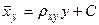где 
– выборочный коэффициент регрессии на .
Пример 1. Найти выборочное уравнение прямой линии регрессии на .
Опытные данные представлены в таблице:
| x | -2 | -1 | ||||
| y | -0,4 | 0,2 | 0,7 | 1,6 | 2,0 | 3,5 |
Проверить адекватность полученной модели.
