Пусть система S с дискретным состоянием Si протекающие значение от 1 до n в котором протекает Марковский случайны процесс с дискретным состоянием и непрерывным. временем.
Записав систему дифференциальных уравнений Колмогорова для вероятности состояния и, проинтегрировав её при заданных начальных условиях получим, N функции.
P1(t),P2(t),…Pn(t),
Для которых выписывается условие
n
∑ Рi(t) = 1
i=1
Поставим вопрос: что будет происходить с системой S при t→∞, будет ли функция Pi(t) стремится к каким-то пределам. эти приделы если они существуют, называются вероятностями состояния Можно доказать следующие положение.
если число состояний системы S конечный из каждого состояния можно перейти за то или другое число шагов в любое другое, то представление вероятности состояний на существование и не зависит от начального состояния системы. Таким образом, при t→∞, в системе S устанавливается предельно стационарный режим. Он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени. Каждое состояние устанавливается с некоторым постоянной вероятностью. Эта вероятность представляет собой относительное время прибивания системы в данном состоянии. Например,если у системы S3 возможных состояния S1,S2,S3. их представления вероятности 0,2; 0,4; 0,4. это означает что после перехода к установившемуся режиму система S в среднем 0,2 времени будет находится состоянии S1и по 0,4 всего времени в состоянии S2,S3. Для вычислительных пределах вероятности состояний нужно в уравнениях Колмогорова все производные прировнять к нулю. При этом система дифференциальных уравнений превращается в систему линейно алгебраического выражения, совместно с условиями
n
∑ = Pi (t) = 1
i=1
Эти уравнения дают вычислить все представленные вероятности состояний Pi(i = 1..n)
Пример:
Определить представление вероятности состояний для системы при следующих интенсивностях перехода.
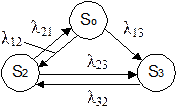
λ12=2
λ21=1
λ13=3
λ23=0,5
λ32=1,5






