Разность потенциалов двух точек поля диполя

Пусть диполь, плечо которого мало (L→0) находится в точке 0 (рис.4).

Вектор Р – электрический момент диполя. α_А - - угол между диполем и направлением на точку А. α_в – угол между диполем и направлением на точку В, r – расстояние от диполя до точек А и В. Используя формулу (5), определим разность потенциалов, создаваемую диполем в точках А и В.

(6)

Обозначим угол между вектором Р и направлением АВ

РОС=α, AOB = ß.

Учитывая эти равенства, выразим α_в=α+

Тогда

Cos (α_в) – Соs(α_A) =-2Sin((α_B+α_A)/2)*Sin((α_B-α_A)/2)=

-2Sin(α+π/2)*Sin(-ß/2)=2Sin(ß/2)*Cos(α).

Подставляя эту формулу в выражение (6), получим:

U_AB= φ_B-φ_A= (7)

Таким образом, создаваемая диполем разность потенциалов двух точек прямо пропорциональна проекции электрического момента диполя, РСоsα на прямую, проходящую через точки А и В. Кроме того она зависит от свойств среды (ε), расстояния этих точек от диполя (~ 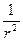) и от угла, под которым эти точки видны от диполя (~Sin ß/2).

Все эти зависимости будут использованы при введении понятия треугольника Эйнтховена(раздел 6.3)