События и величины, используемые в теории надежности, носят случайный характер. Отказы объектов вызываются большим числом причин, связь между которыми установить невозможно, поэтому отказы изделий принадлежат к категории случайных событий. Время до возникновения отказа может принимать различные значения в пределах некоторой области возможных значений и принадлежит к категории случайных величин.
Каждый тип отказов описывается собственной математической моделью, где в качестве основных характеристик является функция распределения времени безотказной работы объекта. Все остальные показатели надежности можно определить по функциям распределения.
Исчерпывающее представление о случайной величине дает закон распределения случайной величины – соотношение между значениями случайной величины и их вероятностями.
Для электротехнических изделий, находящихся в эксплуатации, наиболее часто применяются следующие законы:
- для дискретных случайных величин – биноминальный закон; закон Пуассона;
- для непрерывных случайных величин – экспоненциальный закон; закон нормального распределения (Гаусса); закон Вейбулла; χ2-распределение.
Биноминальный закон. В системах электроснабжения для нормальной эксплуатации используется однотипное оборудование(выключатели, трансформаторы, разъединители и т. п.). Это оборудование может находиться в двух состояниях: работоспособном и неработоспособном.
Если производится n независимых опытов, в каждом из которых событие А появится с вероятностью р, то вероятность того, что событие А появиться ровно m раз, может быть выражено формулой:
, (3.5)
где 
– число слагаемых вида 
, которое равно числу сочетаний.
Вероятность каждой такой комбинации, по теореме умножения для независимых событий, будет равна 
.
Если производится n независимых опытов, в каждом из которых событие А появится с вероятностью p, то вероятность того, что событие А появится ровно m раз, выражается формулой
(3.6)
где 
.
Формула (3.6) является аналитическим выражением искомого закона распределения и носит название формулы Бернулли. В этом выражении коэффициент 
есть коэффициент разложения бинома 
,который по форме представляет собой вероятность 
. Поэтому такое распределение вероятностей называется биноминальным распределением [16].
Свойства данного распределения следующие:
1) число независимых опытов n − целое положительное число;
2) математическое ожидание биноминального распределения 
;
3) центральный момент второго порядка, т.е. дисперсия 
, где 
.
Закон Пуассона. Если случайнаявеличина Х, которая может принимать только целые, неотрицательные значения 0, 1, 2, … и распределена по закону Пуассона, то вероятность того, что на интервале времени t произойдет n случайных событий (отказов) определяется формулой:
, (3.7)
где 
− некоторая положительная величина, называемая параметром закона Пуассона, т.е. среднее число отказов на интервале времени t; е – основание натурального логарифма (е = 2,718...).
Основные числовые характеристики случайной величины Х, наиболее часто используемые и распределенные по закону Пуассона:
–математическое ожидание
, (3.8)
где mх = а, параметр, которыйпредставляет собой не что иное, как математическое ожидание случайной величины Х;
– дисперсия, другая числовая характеристика тоже равна параметру а, т. е. 
.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, будет равна ее математическому ожиданию а.
. (3.9)
Закон Пуассона используется тогда, когда необходимо определить вероятность того, что в системе за данное время произойдет один, два, три и т.д. отказов.
Экспоненциальный закон. Функция распределения случайной величины:
, (3.10)
где λ − интенсивность отказа; t − время возникновения отказа.
Если непрерывная случайная величина Т распределена по показательному закону, то
f(t) = 
(3.11)
а математическое ожидание будет
Таким образом, математическое ожидание показательного распределения равно обратной величине параметраλ, а дисперсия – 
Распределение вероятностей непрерывной случайной величины Т, которое описывается плотностью:
; 
,
это вероятность того, что за время t отказ не возникнет.
Интенсивность отказов λ(t) изменяется во времени следующим образом:
.
Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:
.
Таким образом, признаком экспоненциального закона распределения времени до отказа служит постоянство интенсивности отказов, что характерно для внезапных отказов на интервале времени, когда период приработки объекта закончился, а период износа и старения еще не наступил. Также постоянной становится λ(t) системы, если отказы вызываются отказами большого числа комплектующих элементов, отказ каждого из которых приводит к отказу объекта. Этими факторами, а также тем, что экспоненциальное распределение случайной величины существенно упрощает расчеты надежности, не вызывая значительных погрешностей, обусловлено широкое применение экспоненциального закона в инженерной практике.
Типичная функция интенсивности отказов во времени (в течение срока службы объекта) имеет U -образный характер (см. рис.3.4).
В начальный период I преобладают приработочные отказы. После него наступает наиболее продолжительный период нормальной эксплуатации II, в котором на объект воздействуют случайные факторы. Последние вызывают внезапные отказы, интенсивность которых в период нормальной эксплуатации практически не зависит от времени.
| Рис. 3.4. График функции интенсивности отказов во времени |
III – период аварийного износа, здесь преобладают постепенные отказы.
Учитывая, что для объектов СЭС интенсивность отказов в период нормальной эксплуатации практически неизменна, т. е. 
, соотношения между основными показателями надежности можно представить с учетом этого условия в более простой форме:
; (3.12)
; (3.13)
. (3.14)
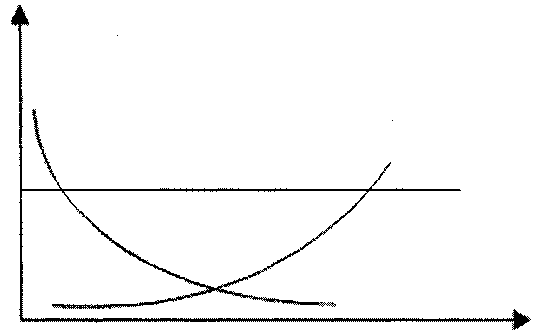
На рисунке 3.5. представлены графики изменения P(t) и Q(T) для экспоненциального закона.
Площадь заштрихованной области между P(t) и осями координат численно характеризует среднюю наработку до отказа Т.
| P,Q Q |
| Q |
| P |
| t |
| T |
Рис. 3.5. Графики вероятности безотказной работы Р (t)и вероятности отказа Q (t) при экспоненциальном законе
Закон нормального распределения (Гаусса) получил наибольшее распространение при оценке надежности СЭС, т.к. он достаточно полно описывает случайные величины массовых явлений.
Значения этих величин зависят от большого числа равно влияющих факторов и обычно равномерно распределяются вокруг среднего значения.
Нормальный закон распределения характеризуется плотностью вероятности вида:
f(t) = 
, (3.15)
Где s и Т – параметры закона распределения (s−среднеквадратическое отклонение t относительно Т, Т – среднее значение t).
Рис.3.6. Плотность распределения нормального закона
При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов.
Вероятность безотказной работы для нормального закона распределения будет определяться по формуле:
P(t) = 1 ‑ 
, (3.16)
а интенсивность отказов − по формуле:
. (3.17)
Исследования показали что нормальное распределение является наиболее приемлемой математической моделью для постепенных отказов при оценке надежности объектов, подверженных действию старения и износа.[23,24]. Он широко используется при анализе безотказности сложных систем на последнем периоде эксплуатации ‑ III (см. рис.3.4.).
| |||||||
| Рис. 3.7. Кривые нормального закона распределения |
Распределение Вейбулла. Модель распределения случайной величины, предложенная шведским ученым Вейбуллом, находит широкое применение ввиду своей простоты и гибкости, так как в зависимости от значений параметров, характер модели видоизменяется. Это распределение чаще всего используется при исследовании интенсивности отказов для периодов приработки и старения, а также при отказах системы, состоящей из последовательно соединенных дублированных элементов.
Она удобна для выбора наиболее подходящего аналитического выражения при определении показателей надежности объекта на основе опытных данных.
Вероятность безотказной работы за время t:
,
где 
− параметры закона распределения.
Функция плотности распределения времени до отказа:
.
Интенсивность отказов:
.
Если 
, то распределение Вейбулла совпадает с экспоненциальным у которого λ=const. Если 
, интенсивность отказов – монотонно убывающая функция; при 
интенсивность отказов − монотонно возрастающая функция (рис. 3.8.).
| |||||
| Рис. 3.8. Зависимость λ = f (t) в модели надежности Вейбулла |
Математическое ожидание или среднее время безотказной работы при распределении по закону Вейбулла:
M = T = Г 
;
где Г(х) – гамма-функция.
χ2-распределение. Возникает при некоторых условиях формирования случайной величины. Если случайная величина t распределена по нормальному закону с параметрами T = 0, s = 1, то 
будет случайной величиной распределенной по закону c2 – распределение, с параметром распределения 
. Параметр k в данном случае равен числу слагаемых.
Отношение удвоенного значения наработки на отказ к средней наработке, т. е. удвоенное число отказов также подчиняется закону c2 –распределения.
Для практического использования c2 – распределения даны в приложении 2.
Из рисунка 3.9. видно, что форма кривых зависит от значения параметра k − числа свободы. Чем меньше k, тем больше c2 – распределение становится несимметричным; чем больше k, тем больше оно приближается к нормальному распределению. При k = 30 его можно считать практически совпадающим с нормальным.
|
Рис.3.9. Плотность распределения χ- квадрат
Чтобы определить значение c2, пользуясь таблицей c2-распределения, необходимо знать число степеней свободы k и 
– уровень значимости или вероятность того, что c2 будет больше найденного значения. Например, при k = 2 и = 0,95 значение c2 = 0,103 (см. приложение 2).
Значения k определяются по определенным правилам. Например, если в качестве c2 используется сумма квадратов 
, тогда для плотности распределения c2 числом степеней свободы k будет число слагаемых.
Если в качестве c2 используется 
(где Т – суммарная наработка изделия; n – суммарное число отказов), тогда числом степеней свободы для f (c2) будет удвоенное число отказов (k = 2 n).
Значение P также выбирается по определенным правилам в каждом конкретном случае использования приложения 2.
